Find the distance of the point (2,3,4) from the plane 3x+2y+2z+5=0 measured parallel to the line x+33=y−26=z2.Solution in Odia
Step by step video & image solution for Find the distance of the point (2,3,4) from the plane 3x+2y+2z+5=0 measured parallel to the line frac[x+3][3]=frac[y-2][6]=frac[z][2]. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Write the value of the following determinant: ∣∣ ∣∣003030300∣∣ ∣∣
View SolutionLet X, Y be non-empty sets such that |X|=m and |Y|=n. If m<n, then how many one-to-one can be defined from X to Y?
View SolutionFind the distance of the point (2,3,4) from the line (x+3)/(3)=(y-2)/(6)=(z)/(2) measured parallel to the plane 3x+2y+2z-5=0
View SolutionFind the distance of the point (2,3,4) from the plane 3x+2y+2z+5=0 measured parallel to the line x+33=y−26=z2.
View Solutionबिन्दु (2,3,4) की समतल 3x+2y+2z+5=0 से दुरी ज्ञात कीजिए जो की रेखा x+33=y−26=z2 एक समान्तर नापी गयी है ।
View Solution(2, 3, 6) என்ற புள்ளி வழிச் செல்வதும் x−12=y+13=z−31 மற்றும் x+32=y−3−5=z+1−3 என்ற கோடுகளுக்கு இணையானதுமான தளத்தின் துணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
View Solutionx−23=y+1−2,z=2 மற்றும் x−11=2y+33,z+52 என்ற கோடுகளுக்கு இடைப்பட்ட கோணம்.
View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
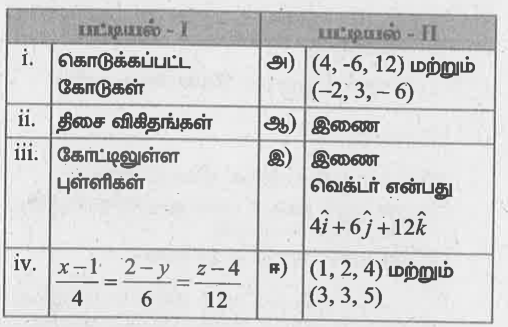
View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
View SolutionFind d.r. of the line 4−x2=y6=1−z3
View SolutionDirection cosines of the line parallel to line x−52=y+3−3=z−56
View SolutionFind the equation of the plane passing through the points (3,4,1) and (0,1,0) and parallel to the line x+32=y−37=z−25.
View SolutionFind the shortest distance between the lines frac[x][2]=frac[y][-3]=frac[z][1] and frac[x-2][3]=frac[y-1][-5]=frac[z+2][2] .
View SolutionFind the equation of the plane passing through the line frac[x+1][-3]=frac[y-3][2]=frac[z+2][1] and the point (0,7,-7). Also show that the line x=frac[7-y][3]=frac[z+7][2] lies in this plane.
View SolutionFind the equation of the plane containing the line frac[x+3][3]=frac[y-1][4]=frac[z-2][-2] and the point (0,2,4).
View Solution
