Convert the followng into products:
(i) sin53∘+sin21∘,(ii)cos83∘−cos17∘,(iii)sin50∘−cos80∘
To convert the given expressions into products, we will use specific trigonometric identities for sums and differences of sine and cosine functions. Let's solve each part step by step.
(i) Convert sin53°+sin21° into products:
1. Identify the formula: We will use the formula for the sum of sines:
\(
\sin A + \sin B = 2 \sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)
\)
2. Assign values: Here, \( A = 53° \) and \( B = 21° \).
3. Calculate \( A + B \) and \( A - B \):
\(
A + B = 53° + 21° = 74°
\)
\(
A - B = 53° - 21° = 32°
\)
4. Substitute into the formula:
\(
\sin 53° + \sin 21° = 2 \sin\left(\frac{74°}{2}\right) \cos\left(\frac{32°}{2}\right)
\)
\(
= 2 \sin(37°) \cos(16°)
\)
Final result for (i):
\(
\sin 53° + \sin 21° = 2 \sin(37°) \cos(16°)
\)
---
(ii) Convert cos83°−cos17° into products:
1. Identify the formula: We will use the formula for the difference of cosines:
\(
\cos A - \cos B = -2 \sin\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)
\)
2. Assign values: Here, \( A = 83° \) and \( B = 17° \).
3. Calculate \( A + B \) and \( A - B \):
\(
A + B = 83° + 17° = 100°
\)
\(
A - B = 83° - 17° = 66°
\)
4. Substitute into the formula:
\(
\cos 83° - \cos 17° = -2 \sin\left(\frac{100°}{2}\right) \sin\left(\frac{66°}{2}\right)
\)
\(
= -2 \sin(50°) \sin(33°)
\)
Final result for (ii):
\(
\cos 83° - \cos 17° = -2 \sin(50°) \sin(33°)
\)
---
(iii) Convert sin50°−cos80° into products:
1. Convert cosine to sine: We know that \( \cos(90° - \theta) = \sin(\theta) \). Thus:
\(
\cos 80° = \sin(10°)
\)
So, we rewrite the expression:
\(
\sin 50° - \cos 80° = \sin 50° - \sin 10°
\)
2. Identify the formula: We will use the formula for the difference of sines:
\(
\sin A - \sin B = 2 \cos\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)
\)
3. Assign values: Here, \( A = 50° \) and \( B = 10° \).
4. Calculate \( A + B \) and \( A - B \):
\(
A + B = 50° + 10° = 60°
\)
\(
A - B = 50° - 10° = 40°
\)
5. Substitute into the formula:
\(
\sin 50° - \sin 10° = 2 \cos\left(\frac{60°}{2}\right) \sin\left(\frac{40°}{2}\right)
\)
\(
= 2 \cos(30°) \sin(20°)
\)
Final result for (iii):
\(
\sin 50° - \cos 80° = 2 \cos(30°) \sin(20°)
\)
---
Summary of Results:
1. \( \sin 53° + \sin 21° = 2 \sin(37°) \cos(16°) \)
2. \( \cos 83° - \cos 17° = -2 \sin(50°) \sin(33°) \)
3. \( \sin 50° - \cos 80° = 2 \cos(30°) \sin(20°) \)
---
\(
\sin A + \sin B = 2 \sin\left(\frac{A+B}{2}\right) \cos\left(\frac{A-B}{2}\right)
\)
\(
A + B = 53° + 21° = 74°
\)
\(
A - B = 53° - 21° = 32°
\)
\(
\sin 53° + \sin 21° = 2 \sin\left(\frac{74°}{2}\right) \cos\left(\frac{32°}{2}\right)
\)
\(
= 2 \sin(37°) \cos(16°)
\)
\(
\sin 53° + \sin 21° = 2 \sin(37°) \cos(16°)
\)
\(
\cos A - \cos B = -2 \sin\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)
\)
\(
A + B = 83° + 17° = 100°
\)
\(
A - B = 83° - 17° = 66°
\)
\(
\cos 83° - \cos 17° = -2 \sin\left(\frac{100°}{2}\right) \sin\left(\frac{66°}{2}\right)
\)
\(
= -2 \sin(50°) \sin(33°)
\)
\(
\cos 83° - \cos 17° = -2 \sin(50°) \sin(33°)
\)
\(
\cos 80° = \sin(10°)
\)
So, we rewrite the expression:
\(
\sin 50° - \cos 80° = \sin 50° - \sin 10°
\)
\(
\sin A - \sin B = 2 \cos\left(\frac{A+B}{2}\right) \sin\left(\frac{A-B}{2}\right)
\)
\(
A + B = 50° + 10° = 60°
\)
\(
A - B = 50° - 10° = 40°
\)
\(
\sin 50° - \sin 10° = 2 \cos\left(\frac{60°}{2}\right) \sin\left(\frac{40°}{2}\right)
\)
\(
= 2 \cos(30°) \sin(20°)
\)
\(
\sin 50° - \cos 80° = 2 \cos(30°) \sin(20°)
\)
1. \( \sin 53° + \sin 21° = 2 \sin(37°) \cos(16°) \)
2. \( \cos 83° - \cos 17° = -2 \sin(50°) \sin(33°) \)
3. \( \sin 50° - \cos 80° = 2 \cos(30°) \sin(20°) \)
Topper's Solved these Questions
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5(A)
49 Videos
- COMPOUND AND MULTIPLE ANGLES BOOK - ICSECHAPTER - COMPOUND AND MULTIPLE ANGLES EXERCISE - EXERCISE 5 (B)
35 Videos
- COMPLEX NUMBERSBOOK - ICSECHAPTER - COMPLEX NUMBERSEXERCISE - Chapter Test
25 Videos
- CONIC SECTIONS BOOK - ICSECHAPTER - CONIC SECTIONS EXERCISE - Multiple Choice Questions
33 Videos
Similar Questions
Find the value of :
(i) sin30∘−cos60∘ (ii) sin0∘+cos0∘
View SolutionFind the value of :
(i) sin30∘+cos60∘ (ii) sin0∘−cos0∘
View Solutioncos17∘+sin17∘cos17∘−sin17∘=tan62∘
View SolutionFind the values of:
(i) tan(−30∘) (ii) sin120∘ (iii) sin135∘ (iv) cos150∘ (v) sin270∘ (vi) cos270∘
View SolutionFind the values of :
(i) tan(−30∘)
(ii) sin120∘
(iii) sin135∘
(iv) cos150∘
(v) sin270∘
(vi) cos270∘
View SolutionConvert the sums or differences into products:
sin61∘−cos39∘
View SolutionConvert the sums or differences into products:
sin4x+cos2x
View SolutionEvaluate:
(i) sin263∘+sin227∘cos217∘+cos273∘
(ii) sin25∘cos65∘+cos25∘sin65∘
View SolutionConvert the products into sum or difference.
2sin48∘cos12∘
View SolutionFind the resultant of the following forces.
[sin37∘=35,cos37∘=45,sin53∘=45,cos53∘=35]
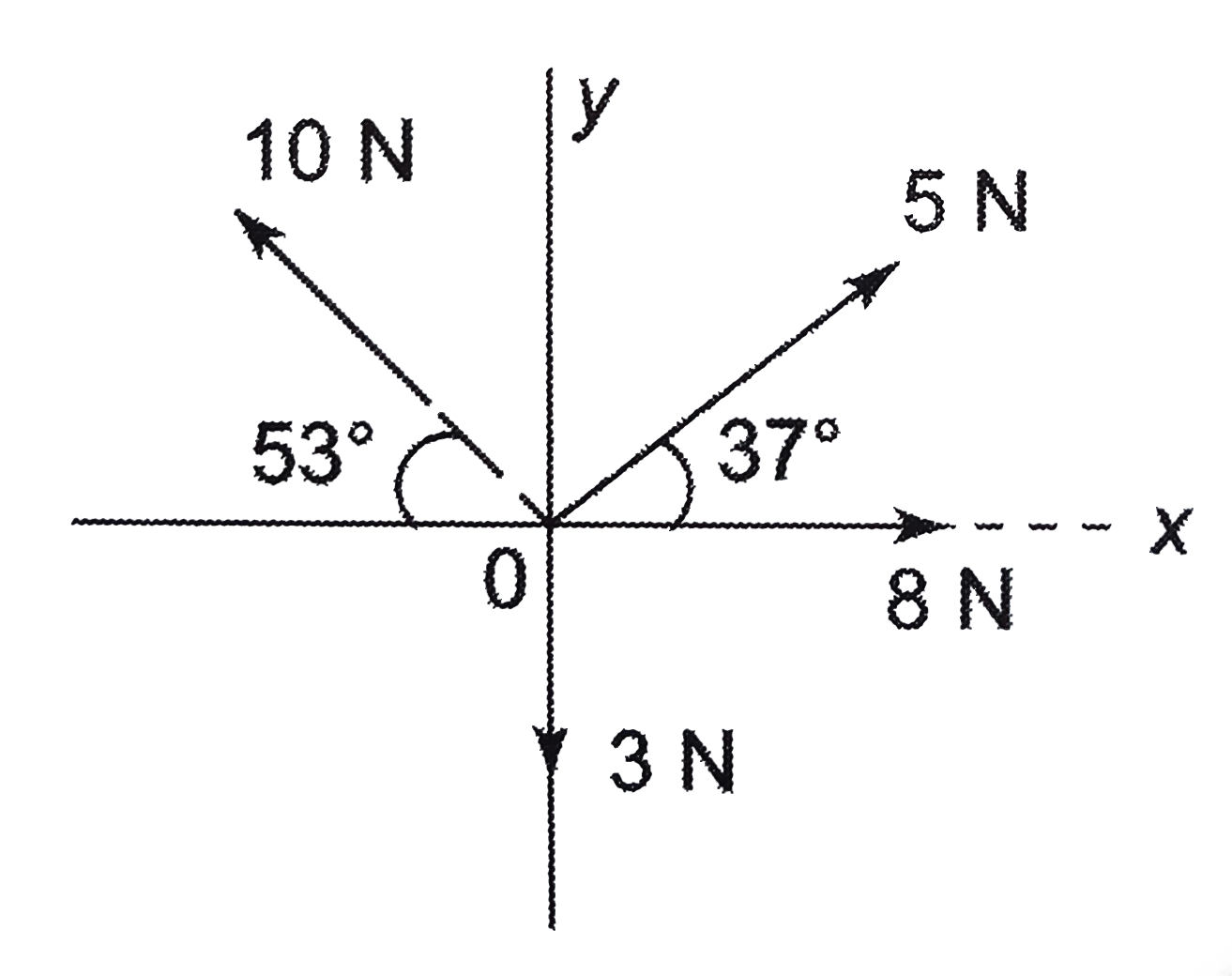
View Solution
