Let y=x+1x.Find the rate of change of y w.r.t. x at x=2.
The correct Answer is:=1−1x2.
To find the rate of change of y with respect to x at x=2 for the function y=x+1x, we will follow these steps:
Step 1: Write down the function
We are given:
y=x+1x
Step 2: Differentiate y with respect to x
To find the rate of change, we need to differentiate y:
dydx=ddx(x+1x)
Step 3: Apply the differentiation rules
Using the sum rule of differentiation, we differentiate each term:
- The derivative of x is 1.
- The derivative of 1x can be rewritten as x−1. Using the power rule, we have:
ddx(x−1)=−1⋅x−2=−1x2
Thus, we have:
dydx=1−1x2
Step 4: Evaluate the derivative at x=2
Now we substitute x=2 into the derivative:
dydx∣∣∣x=2=1−122=1−14
Calculating this gives:
dydx∣∣∣x=2=1−0.25=0.75=34
Final Answer
The rate of change of y with respect to x at x=2 is:
34
---
We are given:
y=x+1x
To find the rate of change, we need to differentiate y:
dydx=ddx(x+1x)
Using the sum rule of differentiation, we differentiate each term:
- The derivative of x is 1.
- The derivative of 1x can be rewritten as x−1. Using the power rule, we have:
ddx(x−1)=−1⋅x−2=−1x2
Thus, we have:
dydx=1−1x2
Now we substitute x=2 into the derivative:
dydx∣∣∣x=2=1−122=1−14
Calculating this gives:
dydx∣∣∣x=2=1−0.25=0.75=34
The rate of change of y with respect to x at x=2 is:
34
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DIFFERENTIATIONEXERCISE - EXERCISE 19 (a)12videos
DIFFERENTIATION
- BOOK - ICSECHAPTER - DIFFERENTIATIONEXERCISE - EXERCISE 19 (b)26videos
DIFFERENTIATION
- BOOK - ICSECHAPTER - CORRELATION ANALYSISEXERCISE - Multiple Choice Question7videos
CORRELATION ANALYSIS
- BOOK - ICSECHAPTER - ELLIPSEEXERCISE - CHAPTER TEST10videos
ELLIPSE
Similar Questions
Let y=ax3+bx2+cx+d. Find the rate of change of y w.r.t x at x=0.
View SolutionLet y=(x+1x)2Find the rate of change of y with respect to x when x=2.
View SolutionLet y=x+3x.Find the instantaneous rate of change of y with respect to x at x = 3.
View SolutionFind the derivative of ex(x2+1) w.r.t. x
View SolutionLet y=x23+2x2.Find the instantaneous rate of change of y with respect to x at x = 1.
View SolutionFind the derivative of xx−2sinx w.r.t. x
View SolutionFind the rate of change of y with respect to xwhen x=1,given that y=x2
View SolutionThe following curve represents rate of change of a variable y w.r.t. x. The change in the value of y when x changes from 0 to 11 is :
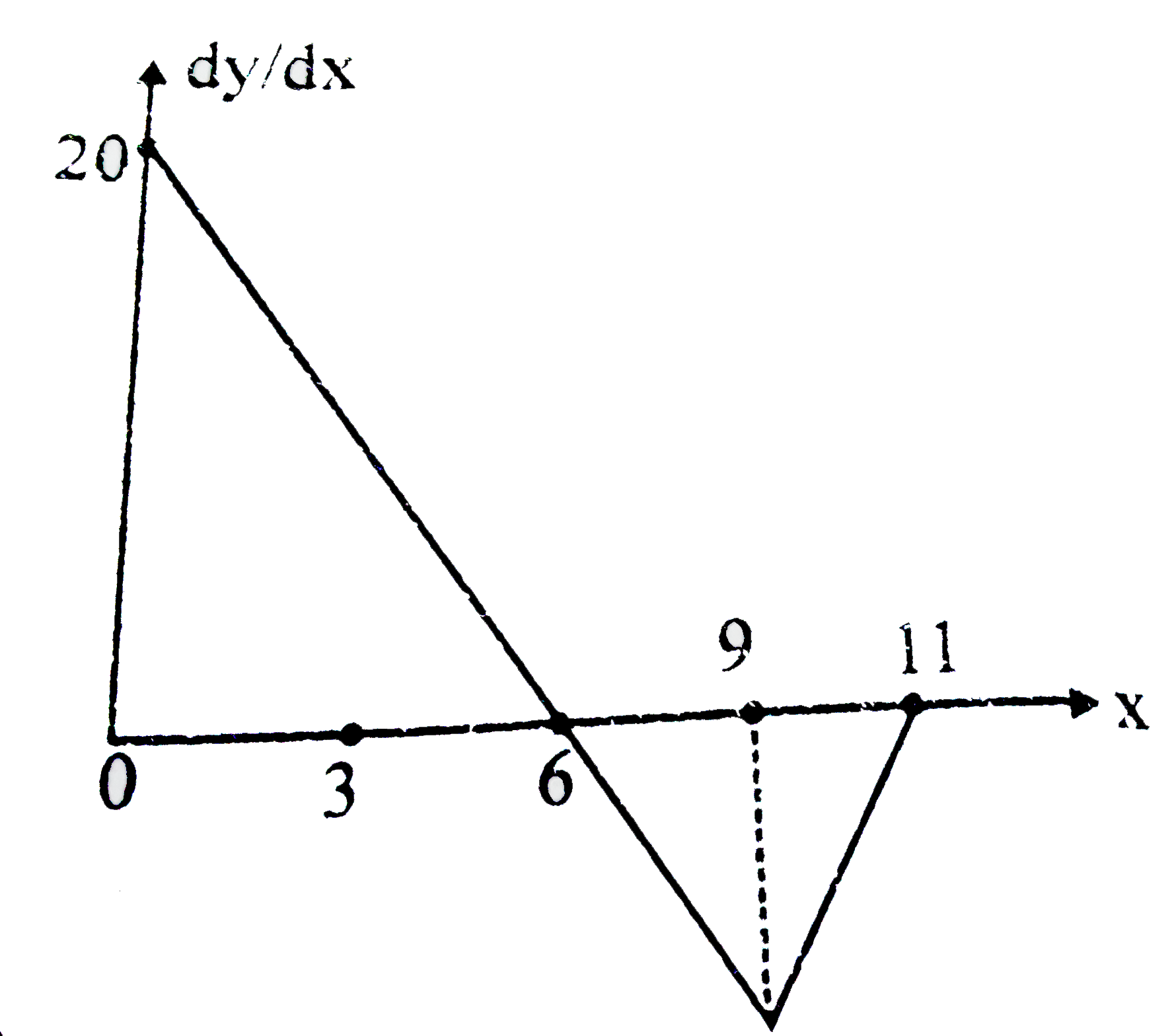 View Solution
View SolutionPoint of contact of y=1-x w.r.t. y2−y+x=0 is
View SolutionFind the polar of the point (1,2) w.r.t the circle x2+y2=7 .
View Solution

