From the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
15, 17, 19, 25, 30, 35, 48
The correct Answer is:M.D = 9.14, coefft. of M.D = 0.338
To solve the problem of calculating the mean deviation and the coefficient of mean deviation from the given data, we will follow these steps:
Step 1: Write down the data
The data provided is:
15,17,19,25,30,35,48
Step 2: Calculate the Mean
The mean (¯x) is calculated using the formula:
¯x=Sum of observationsNumber of observations
- Sum of observations:
15+17+19+25+30+35+48=189
- Number of observations:
There are 7 observations.
Now, substituting these values into the mean formula:
¯x=1897=27
Step 3: Calculate the Mean Deviation
Mean deviation (MD) is calculated using the formula:
MD=∑|xi−¯x|n
where xi are the observations, ¯x is the mean, and n is the number of observations.
- Calculate |xi−¯x| for each observation:
|15−27|=12
|17−27|=10
|19−27|=8
|25−27|=2
|30−27|=3
|35−27|=8
|48−27|=21
- Sum of absolute deviations:
12+10+8+2+3+8+21=64
- Mean Deviation:
MD=647≈9.14
Step 4: Calculate the Coefficient of Mean Deviation
The coefficient of mean deviation (CMD) is calculated using the formula:
CMD=MD¯x
Substituting the values we found:
CMD=9.1427≈0.338
Final Results
- Mean: 27
- Mean Deviation: 9.14
- Coefficient of Mean Deviation: 0.338
The data provided is:
15,17,19,25,30,35,48
The mean (¯x) is calculated using the formula:
¯x=Sum of observationsNumber of observations
15+17+19+25+30+35+48=189
There are 7 observations.
¯x=1897=27
Mean deviation (MD) is calculated using the formula:
MD=∑|xi−¯x|n
where xi are the observations, ¯x is the mean, and n is the number of observations.
|15−27|=12
|17−27|=10
|19−27|=8
|25−27|=2
|30−27|=3
|35−27|=8
|48−27|=21
12+10+8+2+3+8+21=64
MD=647≈9.14
The coefficient of mean deviation (CMD) is calculated using the formula:
CMD=MD¯x
CMD=9.1427≈0.338
- Mean: 27
- Mean Deviation: 9.14
- Coefficient of Mean Deviation: 0.338
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - EXERCISE 21 (b)19videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - CHAPTER TEST6videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF DISPERSIONEXERCISE - CHAPTER TEST6videos
MEASURES OF DISPERSION
- BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCYEXERCISE - EXERCISE14videos
MEASURES OF CENTRAL TENDENCY
- BOOK - ICSECHAPTER - MOCK TEST PAPER-2021EXERCISE - SECTION - C10videos
MOCK TEST PAPER-2021
Similar Questions
From the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
21, 23, 25, 28, 30, 32, 38, 39, 46, 48View SolutionFrom the following data, using mean, calculate mean deviation and the coefficient of mean deviation.
10, 70, 50, 53, 20, 95, 42, 60, 48, 80View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
 View Solution
View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
 View Solution
View SolutionFor the following, using median, calculate mean deviation and coefficient of mean deviation.
100, 150, 200, 250, 360, 490, 500, 600, 671View SolutionFor the following, calculate mean deviation and coefficient of mean deviation.
3, 9, 5, 3, 12, 10, 18, 4, 7, 19, 21View SolutionCalculate the mean deviation and coefficient of mean deviation for the following distribution:
 View Solution
View SolutionIf the mean deviation from the median is 15 and median is 450, then find the coefficient of mean deviation.
View SolutionFind the mean from the following table using step deviation method :
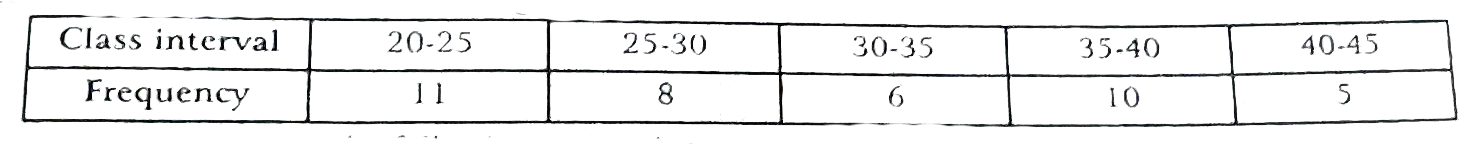 View Solution
View SolutionFind the mean from the following table using step deviation method :
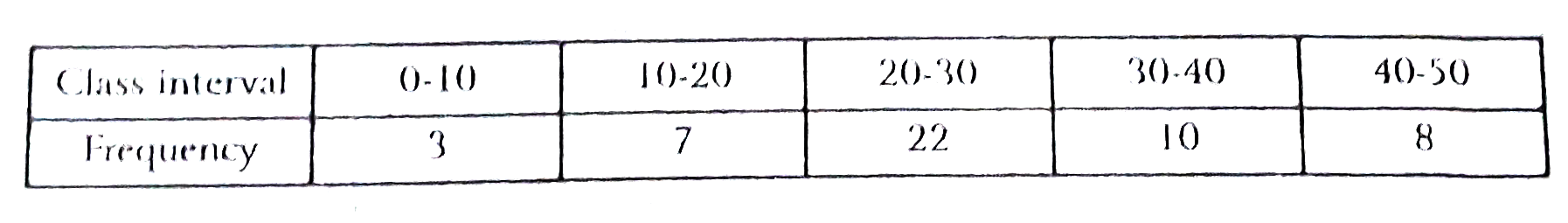 View Solution
View Solution

