Applying to the system two force couples having torques equal in magnitude and opposite in sign,
Text Solution
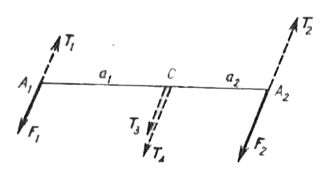
The solid arrows in Fig. show the forces F1 and F2 applied to a rigid body at points A1andA2 Apply the forces T1andT2 at the same points and the forces T3andT4 at the point C so that is T1=T3=F1andT2=T4=F2 . The point C is chosen so that F1a1=Fyay . Show that the now nystem of six forces is equivalent to the old one, i.e. that
(F1,F2,T1,T2,T3,T4)~(F1,F2)
Indeed, the system of these forces reduces to the former forces F1andF2 and to two force couples (T1,T3)and(T2,T4) whose moments are
M1=T1a1sinαandM2=−T2a2sinα
But point was chosen go that |M1|=|M2| Therefore these moments are compensated and do not act on the rigid body.
On the other hand, the system of six forces is equivalent to the system of forces T3andT4 , i.e.
(F1,F2,T1,T2,T3,T4)~(T3,T4)
Indeed, the forces F1 and T1 , as well as F1andT2 are compensated, only the forces T3andT4 remaining uncompensated.
Hence, the system of forces (F1,F2) is equivalent to the system (T3T4) , and this gives the solution to the problem.
|
Similar Questions
Knowledge Check
Find the equation of the straight line making intercepts on the axes equal in magnitude and both positive and passing through the point (5,6) :
Aa. x+y=11Bb. 2x+y=3Cc. x-y=3Dd. none of theseTwo measurements of a cylinder are varying in such a way that the volume is kept constant. If the rates of change of the radius (r ) and height (h) are equal in magnitude but opposite in sign, then
Ar=2hBh=2rCh=rDh=2r
For what value of m the roots of the equation I are equal in magnitude and opposite in signs?
View SolutionIf roots of ax2+bx+c=0 are equal in magnitude but opposite in sign, then
View SolutionEquation of straight line passing through (2,1) and having intercepts equal in magnitude but opposite in sign in
View SolutionIf roots of ax2+bx+c=0 are equal in magnitude but opposite in sign, then
View SolutionFind the equation of a line which passes through the point (5,1) and cuts, equal in magnitude but opposite in sign, intercepts on axes.
View SolutionTwo measurements of a cylinder are varying in such a way that the volume is kept constant. If the rates of change of the radius (r ) and height (h) are equal in magnitude but opposite in sign, then
View Solution
