For a thin-walled solid cylinder of the same radius and mass.
The correct Answer is:2.3 m/s
v=√g(lsinα+rcosα−lkcosαr)
Similar Questions
A solid hemisphere of radius R is mounted on a solid cylinder of same radius and density as shown .the height of cylinder is such that the resulting centre of mass is at O. if radius of sphrere is 2√2m, what is the height of the cylinder (in m ) ?
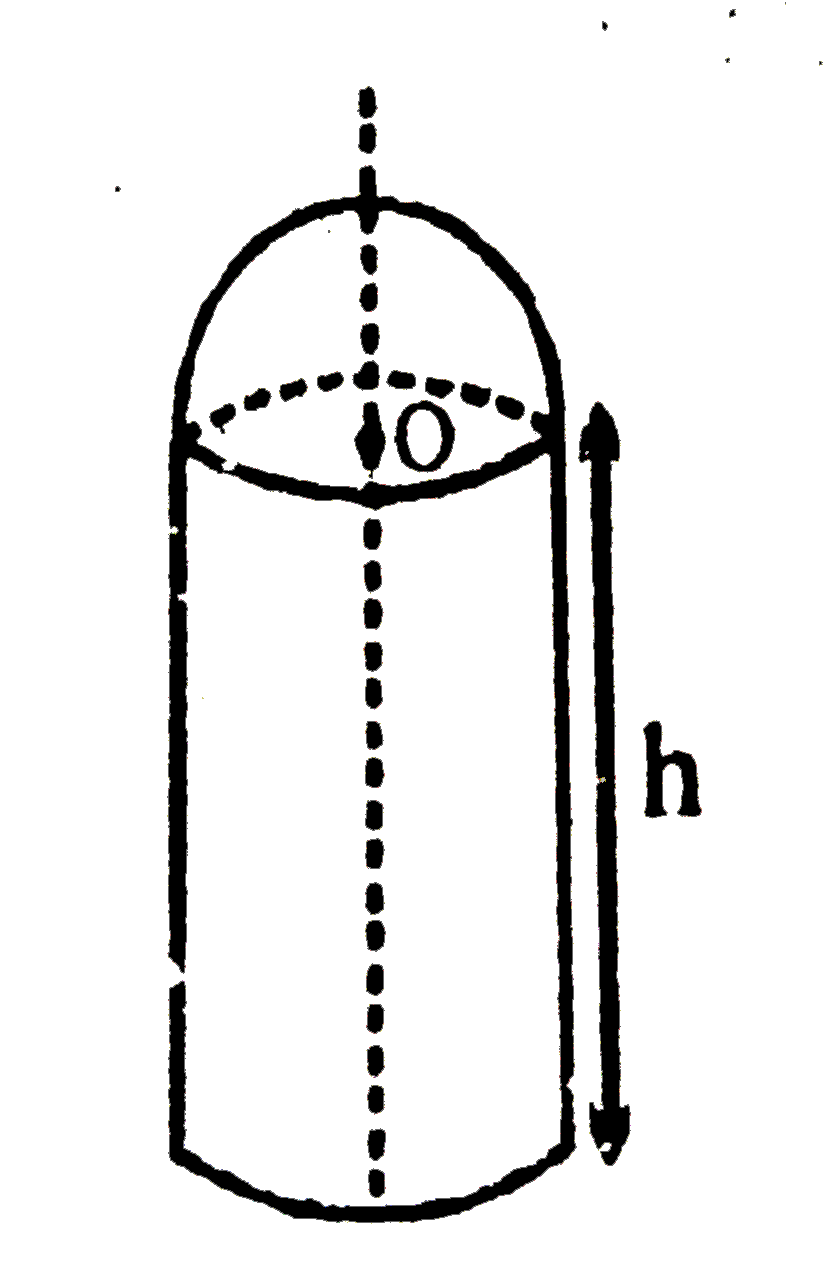
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
View Solution
Knowledge Check
A solid cylinder and a thin-walled hollow cylinder have the same mass and radius. They are rolling horizontally toward the bottom of an incline. The center of mass of each has the same translational speed. The cylinders roll up the incline and reach their highest points. Calculate the ratio of the distances (SSolid/Shollow) along the incline through which each center of mass moves.
A43B34C23D32A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere/Ecylinder) will be
A3:1B2:3C1:5D1:4A solid sphere of mass m and radius R is rotating about its diameter A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere . The ratio of their kinetic energies of rotation (Esphere/Ecylinder) will be
A2:3B1:5C1:4D3:1
Find the self gravitationl potential of (a) a thin unifrom spherical shell of radius R snd mass M, (b) a solid sphere of the same radius and mass .
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere/Ecylinder) will be
View SolutionA hoop and a solid cylinder have the same mass and radius. They both roll,without slipping, on horizontal surface. If their kinetic energies are equal -
View Solution
