Find the value of x in each of the following :
42 : 12 : : 7 : x
The correct Answer is:x = 2
To find the value of x in the proportion 42:12::7:x, we can set up the equation based on the definition of ratios.
1. Set Up the Proportion:
The given ratio can be expressed as:
4212=7x
2. Cross Multiply:
To eliminate the fractions, we cross multiply:
42⋅x=12⋅7
3. Calculate the Right Side:
Now, calculate 12⋅7:
12⋅7=84
So, we have:
42x=84
4. Solve for x:
To find x, divide both sides by 42:
x=8442
5. Simplify the Fraction:
Simplifying 8442:
x=2
Final Answer:
The value of x is 2.
The given ratio can be expressed as:
4212=7x
To eliminate the fractions, we cross multiply:
42⋅x=12⋅7
Now, calculate 12⋅7:
12⋅7=84
So, we have:
42x=84
To find x, divide both sides by 42:
x=8442
Simplifying 8442:
x=2
The value of x is 2.
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Example
20 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Try This!
29 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise 7 A
38 Videos
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B
10 Videos
- RATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL NUMBERS EXERCISE - REVISION EXERCISE (FILL IN THE BOXES).
4 Videos
Similar Questions
Find the value of x in each of the following :
16:x::x:25
View SolutionFind the value of x in each of the following :
6 : 0.8 : : x : 10
View SolutionFind the value of x in each of the following figures.
View SolutionFind the value of x in each of the following figures.
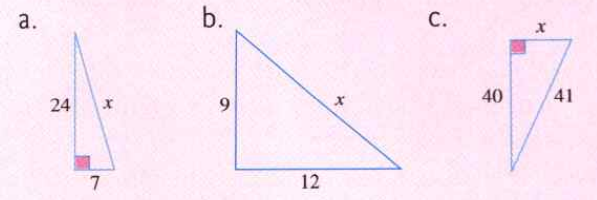
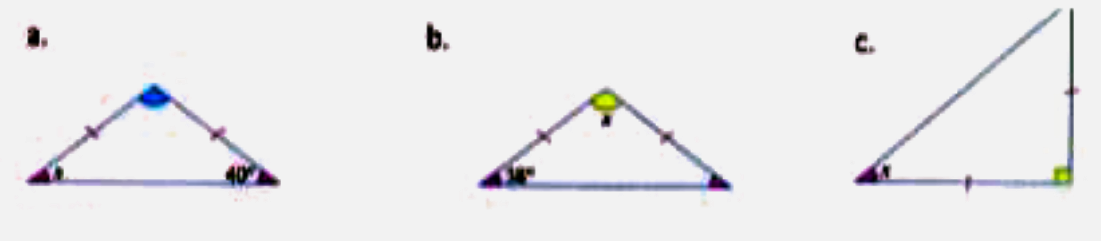
View SolutionFind the value of x in each of the following triangles.
View SolutionFind the value of x in each of the following figures if l∣∣m.
View SolutionFind the values of x and y in each of the following diagrams :
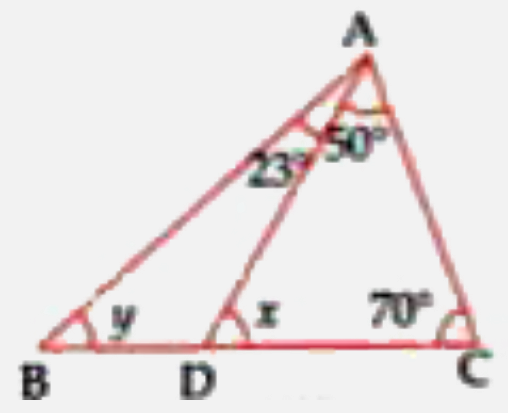
View SolutionFind the values of x and y in each of the following diagrams :
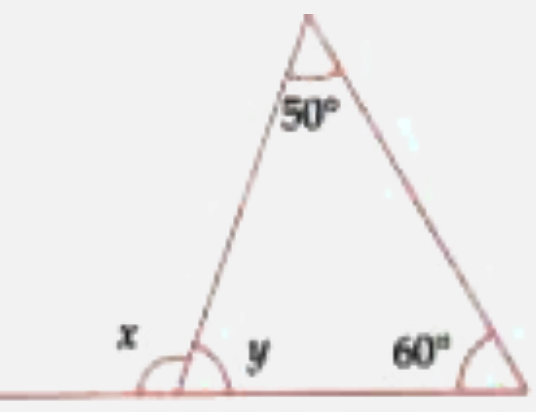
View SolutionFind the values of x and y in each of the following diagrams :
View SolutionFind the value of x in each of the following: 2x−7 × 5x−4=1250 (ii) (4)2x+12=132
View Solution
