Construct a straight line cm Draw its line of symmetry (using a pair of compasses).
Step-by-Step Solution:
1. Draw the Line Segment AB:
- Use a ruler to draw a straight line segment AB that measures 7.3 cm. Label the endpoints as A and B.
Hint: Ensure that you measure accurately using the ruler to get the exact length of 7.3 cm.
2. Find the Midpoint:
- To find the midpoint of line segment AB, we need to open the compass to more than half the length of AB. Since AB is 7.3 cm, open the compass to a little more than 3.65 cm.
Hint: Remember that the midpoint is the point that divides the line segment into two equal parts.
3. Draw Arcs from Point A:
- Place the compass point on point A and draw an arc above and below the line segment.
Hint: Make sure the compass remains at the same width while drawing the arcs.
4. Draw Arcs from Point B:
- Now, without changing the compass width, place the compass point on point B and draw another arc above and below the line segment, ensuring that these arcs intersect the arcs drawn from point A.
Hint: The arcs should intersect at two points, one above and one below the line segment.
5. Label the Intersection Points:
- Label the points where the arcs intersect as C and D.
Hint: These points are crucial as they will help in drawing the perpendicular bisector.
6. Draw the Perpendicular Bisector:
- Using a ruler, draw a straight line connecting points C and D. This line is the perpendicular bisector of line segment AB and acts as the line of symmetry.
Hint: Ensure that the line you draw is straight and extends sufficiently to show it clearly.
7. Final Check:
- Verify that the line CD divides the segment AB into two equal parts, confirming that it is indeed the line of symmetry.
Hint: Measure the lengths AC and CB to ensure they are equal.
Summary of Steps:
- Draw line segment AB = 7.3 cm.
- Open compass to more than half the length of AB.
- Draw arcs from points A and B.
- Mark intersection points of arcs.
- Draw the line connecting intersection points to complete the perpendicular bisector.
- Use a ruler to draw a straight line segment AB that measures 7.3 cm. Label the endpoints as A and B.
- To find the midpoint of line segment AB, we need to open the compass to more than half the length of AB. Since AB is 7.3 cm, open the compass to a little more than 3.65 cm.
- Place the compass point on point A and draw an arc above and below the line segment.
- Now, without changing the compass width, place the compass point on point B and draw another arc above and below the line segment, ensuring that these arcs intersect the arcs drawn from point A.
- Label the points where the arcs intersect as C and D.
- Using a ruler, draw a straight line connecting points C and D. This line is the perpendicular bisector of line segment AB and acts as the line of symmetry.
- Verify that the line CD divides the segment AB into two equal parts, confirming that it is indeed the line of symmetry.
- Draw line segment AB = 7.3 cm.
- Open compass to more than half the length of AB.
- Draw arcs from points A and B.
- Mark intersection points of arcs.
- Draw the line connecting intersection points to complete the perpendicular bisector.
Topper's Solved these Questions
Similar Questions
Draw the lines of symmetry for the following figures.
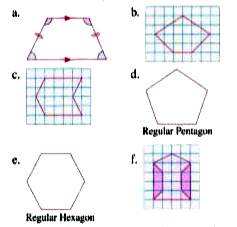 .
.
View SolutionDraw the lines of symmetry of the following figures.
 .
.
View SolutionDraw the lines of symmetry for the following shapes:
 .
.
View SolutionDraw the lines of symmetry of each of the following shapes.
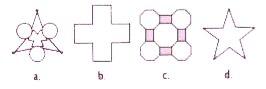 .
.
View SolutionDraw all possible lines of symmetry in :
a regular pentagon
View SolutionTrace each figure and draw the lines of symmetry, if any:

View SolutionDraw all possible lines of symmetry in :
a regular hexagon
View SolutionDraw a straight line AB=6.5 cm. draw another line which is parallel to AB at a distance of 2.8 cm from it.
View SolutionConstruct a square having each side equal to 4 cm. Draw all possible lines of symmetry.
View SolutionConstruct a quadrilateral with:
a. one line of symmetry.
b. two lines of symmetry.
View Solution
