Add: 63∘45'28''and85∘50'45''
The correct Answer is:149∘36'13''
To solve the problem of adding the angles 63∘45′28′′ and 85∘50′45′′, we will follow these steps:
1. Write down the angles to be added:
- First angle: 63∘45′28′′
- Second angle: 85∘50′45′′
2. Add the seconds:
- 28′′+45′′=73′′
3. Convert seconds to minutes:
- Since 73′′ is more than 60′′, we convert it:
- 73′′=60′′+13′′ which gives us 1′ (1 minute) and 13′′ (13 seconds).
- So, we have 1′ to carry over.
4. Add the minutes including the carry from seconds:
- 45′+50′+1′=96′
5. Convert minutes to degrees:
- Since 96′ is more than 60′, we convert it:
- 96′=60′+36′ which gives us 1∘ (1 degree) and 36′ (36 minutes).
- So, we have 1∘ to carry over.
6. Add the degrees including the carry from minutes:
- 63∘+85∘+1∘=149∘
7. Combine all parts:
- The final result combines degrees, minutes, and seconds:
- 149∘36′13′′
Final Answer:
The sum of 63∘45′28′′ and 85∘50′45′′ is 149∘36′13′′.
---
- First angle: 63∘45′28′′
- Second angle: 85∘50′45′′
- 28′′+45′′=73′′
- Since 73′′ is more than 60′′, we convert it:
- 73′′=60′′+13′′ which gives us 1′ (1 minute) and 13′′ (13 seconds).
- So, we have 1′ to carry over.
- 45′+50′+1′=96′
- Since 96′ is more than 60′, we convert it:
- 96′=60′+36′ which gives us 1∘ (1 degree) and 36′ (36 minutes).
- So, we have 1∘ to carry over.
- 63∘+85∘+1∘=149∘
- The final result combines degrees, minutes, and seconds:
- 149∘36′13′′
The sum of 63∘45′28′′ and 85∘50′45′′ is 149∘36′13′′.
Similar Questions
Add 55∘49'31''and63∘22'45''
View SolutionA liquid cools from 50∘C to 45∘C in 5 minutes and from 45∘C to 41.5∘C in the next 5 minutes. The temperature of the surrounding is
View SolutionAdd :
63.05 , 24.839 , 3.7 , 16.85
View SolutionConstruct a ΔABC in which AB = 6.3 cm, AC = 4.5 cm and ∠A=45∘.
View SolutionExpress the following in terms of angles between 0∘ and 45∘
sin59∘+tan63∘
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.
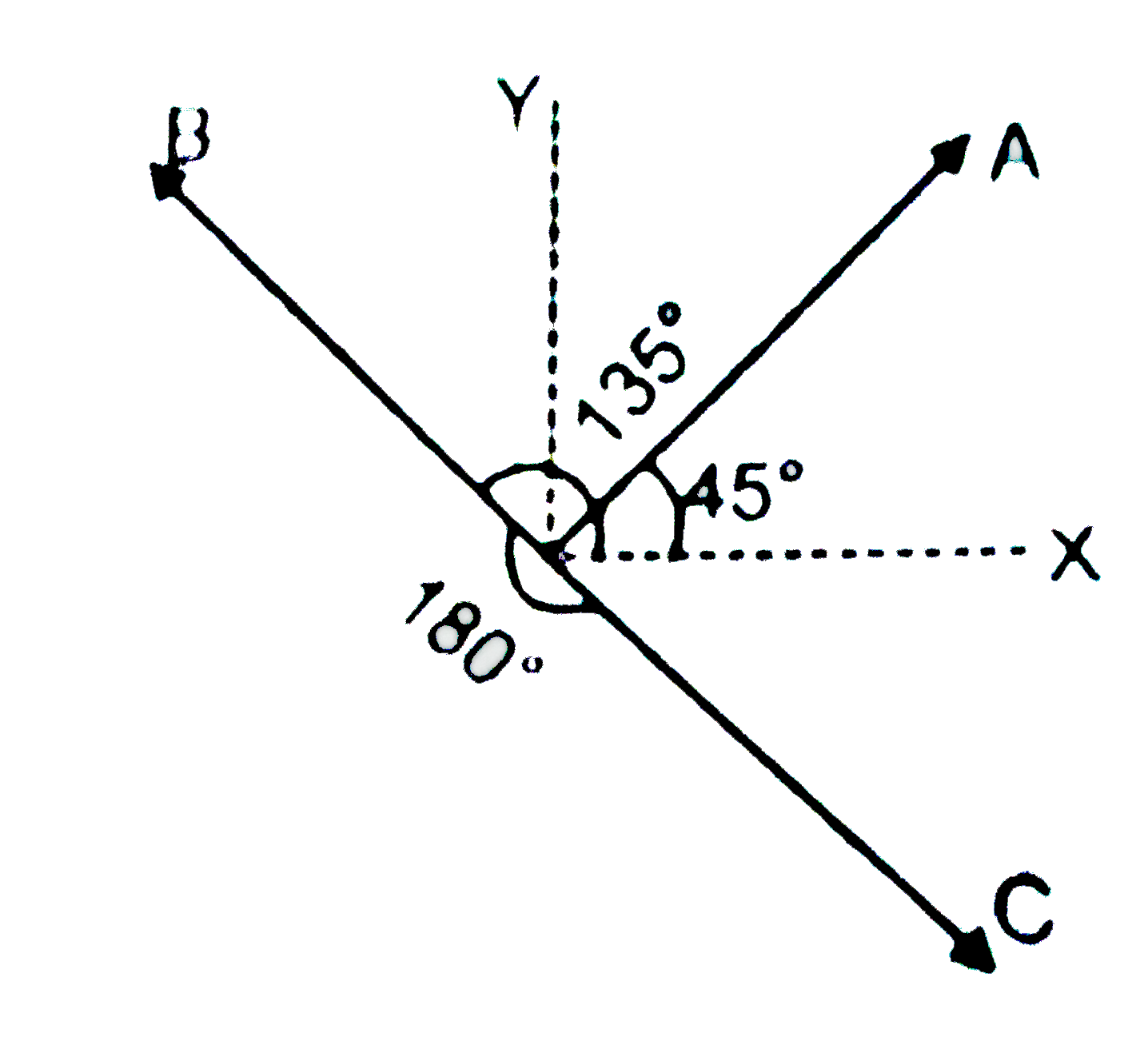
View SolutionAdd vectors →A,→B and →C which have equal magnitude s of 50 unit and are inclined at angles of 45∘,135∘ and 315∘ respectively from x-axos.

View Solutioncos(A+B)+sin(A−B)=2sin(45∘+A)cos(45∘+B).
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionA line through the origin divides parallelogram with vertices (10,45) , (10, 14) , (28,153) and (28,84) into two congruent pieces. The slope of the line is
View Solution
