A man in a boat rows 3 miles off along straight shore and wants to reach a point 4 miles up the shore on the opposite side. If he can row 2 miles/hour and walk 4 miles/hour, describe his fastest route.
The correct Answer is:√3 miles from A
To solve the problem step by step, we will use the information given about the distances and speeds of the man rowing and walking.
Step 1: Understand the Problem
The man is 3 miles off the shore and wants to reach a point 4 miles up the shore. He can row at a speed of 2 miles/hour and walk at a speed of 4 miles/hour.
Step 2: Set Up the Coordinates
Let’s denote:
- The starting point of the man in the boat as point A (0, 0).
- The point directly across the shore (the point he rows to) as point B (3, 0).
- The destination point up the shore as point C (3, 4).
Step 3: Define the Variables
Let x be the distance he rows to a point D on the shore, which is directly across from point B. The coordinates of point D will be (3, y) where y is the distance he rows. The distance he walks from point D to point C will be 4−y.
Step 4: Calculate the Distances
Using the Pythagorean theorem, the distance he rows (AD) can be expressed as:
AD=√(3)2+(y)2=√9+y2
Step 5: Calculate the Time Taken
The time taken to row to point D (t1) is:
t1=DistanceSpeed=√9+y22
The time taken to walk from point D to point C (t2) is:
t2=4−y4
Step 6: Total Time Function
The total time T taken is the sum of the rowing time and walking time:
T=t1+t2=√9+y22+4−y4
Step 7: Differentiate the Total Time
To find the minimum time, we differentiate T with respect to y and set the derivative equal to zero:
dTdy=12⋅12√9+y2⋅2y−14=y2√9+y2−14
Setting dTdy=0:
y2√9+y2=14
Step 8: Solve for y
Cross-multiplying gives:
4y=2√9+y2
Squaring both sides:
16y2=4(9+y2)⟹16y2=36+4y2⟹12y2=36⟹y2=3⟹y=√3
Step 9: Calculate the Distance y
Now substituting y back into the equations:
- The distance he rows is √9+3=√12=2√3.
- The distance he walks is 4−√3.
Final Answer
The fastest route for the man is to row 2√3 miles to the shore and then walk 4−√3 miles to his destination.
The man is 3 miles off the shore and wants to reach a point 4 miles up the shore. He can row at a speed of 2 miles/hour and walk at a speed of 4 miles/hour.
Let’s denote:
- The starting point of the man in the boat as point A (0, 0).
- The point directly across the shore (the point he rows to) as point B (3, 0).
- The destination point up the shore as point C (3, 4).
Let x be the distance he rows to a point D on the shore, which is directly across from point B. The coordinates of point D will be (3, y) where y is the distance he rows. The distance he walks from point D to point C will be 4−y.
Using the Pythagorean theorem, the distance he rows (AD) can be expressed as:
AD=√(3)2+(y)2=√9+y2
The time taken to row to point D (t1) is:
t1=DistanceSpeed=√9+y22
The time taken to walk from point D to point C (t2) is:
t2=4−y4
The total time T taken is the sum of the rowing time and walking time:
T=t1+t2=√9+y22+4−y4
To find the minimum time, we differentiate T with respect to y and set the derivative equal to zero:
dTdy=12⋅12√9+y2⋅2y−14=y2√9+y2−14
Setting dTdy=0:
y2√9+y2=14
Cross-multiplying gives:
4y=2√9+y2
Squaring both sides:
16y2=4(9+y2)⟹16y2=36+4y2⟹12y2=36⟹y2=3⟹y=√3
Now substituting y back into the equations:
- The distance he rows is √9+3=√12=2√3.
- The distance he walks is 4−√3.
The fastest route for the man is to row 2√3 miles to the shore and then walk 4−√3 miles to his destination.
Topper's Solved these Questions
- MODEL TEST PAPER-9BOOK - ICSECHAPTER - MODEL TEST PAPER-9EXERCISE - SECTION - B
10 Videos
- MODEL TEST PAPER-9BOOK - ICSECHAPTER - MODEL TEST PAPER-9EXERCISE - SECTION - C
10 Videos
- MODEL TEST PAPER-6BOOK - ICSECHAPTER - MODEL TEST PAPER-6EXERCISE - Section -C
10 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - MULTIPLE CHOICE QUESTIONS
82 Videos
Similar Questions
A man can row a boat with 4km/h in still water, if he is crossing a river where the current is 2 km/h.
(a) In what direction will his boat be holded, if he wants to reach a point on the other bank, directly opposite to starting point?
(b) If width of the river 4km, how long will the man take to cross the river, with the condition in part (a)?
(c) In what direction shou ld he heat the boat if he wants to cross the river in shorest time and what is this minimum time?
(d) How long will it take him to row 2 km up the stream and then back to his starting point?
View SolutionWidth of a river is 30m, velocity is 4m/s and rowing velocity is 5m/s
(a) Make the velocity diagram for crossing the river in shortest time. Then, find this shortest time, net velocity of boatman and drigt along the river.
(b) Can the boatman reach a point just oppsite on the other shore? If yes then make the velocity diagram, the direction in which the should row his boat and the time taken to cross the river in this case.
(c) How long will it iake hom to row 10m up the stream and then back to his starting point?
View Solution
Knowledge Check
Waugh jogged to a restaurent at x miles per hour, and jogged back home along the same route at y miles per hour. He took 30 minutes for the whole trip. If the restaurant is 2 miles form home along the route he too, what is the average speed in miles per hour at which he jogged for the whole trip ?
A0.13B0.5C2D8Brian plans to complete a 100-mile bike race for charity. According to his registration materials, he will need to ride at an average speed of 12.5 miles per hour if he wants to complete the course before it closes. On a pratice ride the week before the race, Brain rides 60 miles and trackes his speed. For the first 30 miles, his average speed is 16 miles per hour, and for the next 30 miles, his average speed is 15 miles per hour. If Brian can match these speeds for the first 60 miles of the charity race, then he rests for that total of 1 hour after that, what approximately speed must he maintain for the last 40 miles in order to complete the ride on time?
A8 miles per hourB10 miles per hourC13 miles per hourD14 miles per hourA cargo ship is 4.2 miles from a lighthouse, and a fishing boat is 5.0 miles from the lighthouse, as shown below. The angle between the straight lines from the lighthouse to the 3 vessels is 5∘. The approximate distance in miles, from the cargo ship to the fishing boat is given by which of the following expressions?
(Note: The law of cosines states that for any triangle with vertices A, B and C adn the sides opposite those vertices with length a, b, and c, respectively. c2=a2+b2−2abcosC).
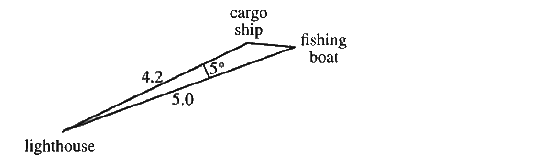 A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A√(5.0)2−(4.2)2B√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos5∘C√(4.2)2+(5.0)2+2⋅4.2⋅5.0cos5∘D√(4.2)2+(5.0)2−2⋅4.2⋅5.0cos85∘
A man who swims at a speed of 5km/h wants to cross a 500m wide stream flowing at 4km/h and reach the point which is directly opposite to his starting point. If he reaches a point somewhere else he has to walk back to desitination, his walking speed being 2km/h. Find the minimum time in which he can reah his destination.

View SolutionRory left home and drove straight to the airport at an average speed of 45 miles per hour. He returned home along the same route, but traffic slowed him down and he only averaged 30 miles per hour on the return trip. If his total travel time was 2 hours and 30 minutes, how far is it, in miles, from Rory's house to the airport?
View SolutionDoes the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View SolutionA straight road is at a distance of 5√2 miles from a place. The shortest distance of the road from the place is in the N.E. direction. Do the following villages which (i) is 6 miles East and 4 miles North from the place lie on the road or no, (ii) is 4 miles East and 3 miles North from the place, lie on the road or not?
View SolutionA boat man could row his boat with a speed 10 m/sec. He wants to take his boat from P to a point Q just opposite on the other bank of the river flowing at a speed 4 m/sec. He should row his boat–
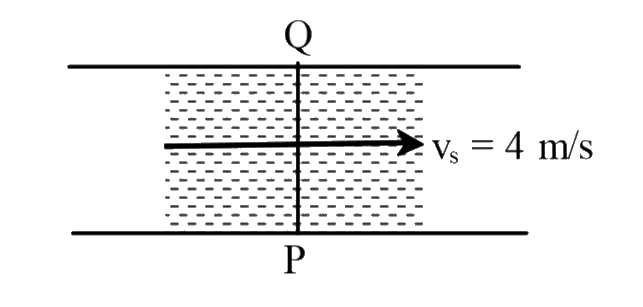
View Solution
