The length of the perimeter of a sector of a circle is 20 cm. Give an expression for the area of the sector in terms of r(the radius of the circle) and hence find the maximum area of the sector.
The correct Answer is:
To solve the problem step by step, we will follow the instructions provided in the video transcript.
Step 1: Understanding the Perimeter of the Sector
The perimeter of a sector of a circle is given by the formula:
Perimeter=2r+rθ
where r is the radius and θ is the angle in radians. We are given that the perimeter is 20 cm:
2r+rθ=20
Step 2: Rearranging the Equation
We can rearrange this equation to express r in terms of θ:
r(2+θ)=20
r=202+θ(1)
Step 3: Finding the Area of the Sector
The area A of the sector can be expressed as:
A=12r2θ
Substituting the expression for r from equation (1):
A=12(202+θ)2θ
A=12⋅400(2+θ)2⋅θ
A=200θ(2+θ)2
Step 4: Maximizing the Area
To find the maximum area, we need to differentiate A with respect to θ and set the derivative equal to zero:
dAdθ=0
Using the quotient rule:
dAdθ=(2+θ)2⋅200−200θ⋅2(2+θ)(2+θ)4
Setting the numerator equal to zero:
200(2+θ)2−400θ(2+θ)=0
200(2+θ)(2+θ−2θ)=0
200(2+θ)(2−θ)=0
This gives us θ=2 (since 2+θ≠0).
Step 5: Confirming Maximum Area
To confirm that this is a maximum, we can check the second derivative or simply evaluate the first derivative around θ=2. However, we can directly substitute θ=2 back into the area formula:
r=202+2=204=5
Now substituting θ=2 into the area formula:
A=200⋅2(2+2)2=40016=25 cm2
Final Result
The maximum area of the sector is:
25 cm2
The perimeter of a sector of a circle is given by the formula:
Perimeter=2r+rθ
where r is the radius and θ is the angle in radians. We are given that the perimeter is 20 cm:
2r+rθ=20
We can rearrange this equation to express r in terms of θ:
r(2+θ)=20
r=202+θ(1)
The area A of the sector can be expressed as:
A=12r2θ
Substituting the expression for r from equation (1):
A=12(202+θ)2θ
A=12⋅400(2+θ)2⋅θ
A=200θ(2+θ)2
To find the maximum area, we need to differentiate A with respect to θ and set the derivative equal to zero:
dAdθ=0
Using the quotient rule:
dAdθ=(2+θ)2⋅200−200θ⋅2(2+θ)(2+θ)4
Setting the numerator equal to zero:
200(2+θ)2−400θ(2+θ)=0
200(2+θ)(2+θ−2θ)=0
200(2+θ)(2−θ)=0
This gives us θ=2 (since 2+θ≠0).
To confirm that this is a maximum, we can check the second derivative or simply evaluate the first derivative around θ=2. However, we can directly substitute θ=2 back into the area formula:
r=202+2=204=5
Now substituting θ=2 into the area formula:
A=200⋅2(2+2)2=40016=25 cm2
The maximum area of the sector is:
25 cm2
Topper's Solved these Questions
- MODEL TEST PAPER-11BOOK - ICSECHAPTER - MODEL TEST PAPER-11EXERCISE - SECTION-B
10 Videos
- MODEL TEST PAPER-11BOOK - ICSECHAPTER - MODEL TEST PAPER-11EXERCISE - SECTION-C
9 Videos
- MODEL TEST PAPER 20 BOOK - ICSECHAPTER - MODEL TEST PAPER 20 EXERCISE - SECTION C
10 Videos
- MODEL TEST PAPER-12 BOOK - ICSECHAPTER - MODEL TEST PAPER-12 EXERCISE - SECTION-C
10 Videos
Similar Questions
The perimeter of a sector of a circle of radius 5.2cm is 16.4cm. Find the area of the sector.
View SolutionThe perimeter of a sector a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. find the area of the sector
View SolutionThe perimeter of a certain sector of a circle of radius 5.6 m is 27.2 m. Find the area of the sector
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
View SolutionWhat is the area of the sector shown in
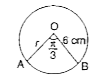
View SolutionFind the area of a sector of a circle with radius 6 cm if angle of the sector is 60∘
View SolutionThe area of a sector of a circle 2 cm is π cm2 . Find the angle contained by the sector
View SolutionA sector of a circle of radius 8 cm contains an angle of 135o . Find the area of the sector.
View SolutionIf the perimeter of a certain sector of a circle is equal to the length of the arc of the semicircle having the same radius , find the angle of the sector in degrees .
View Solution
