There are two types of fertilizers F1 and F2.F1 consists of 10% nitrogen and 6% phosphoric acid and F2 contains 5% nitrogen and 10% phosphoric acid. After testing the soil condition a farmer finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid forhis crop. If F1 costs Rs. 6 per kg and F2 costs Rs. 5 perkg, determine how muchofeach of fertilizers beused so that nutrient requirements are met at a minimum cost. What is the minimum cost?
The correct Answer is:80 kg of fertilizer F1 and 100 kg of fertilizer F2
Minimum cos = Rs. 980
To solve the problem, we need to set up a system of equations based on the information provided about the fertilizers and the requirements for nitrogen and phosphoric acid. Let's break this down step by step.
Step 1: Define Variables
Let:
- x = amount (in kg) of fertilizer F1
- y = amount (in kg) of fertilizer F2
Step 2: Write Down the Nutrient Content
From the problem, we know:
- Fertilizer F1 contains:
- 10% nitrogen
- 6% phosphoric acid
- Fertilizer F2 contains:
- 5% nitrogen
- 10% phosphoric acid
Step 3: Set Up the Constraints
The farmer needs at least:
- 14 kg of nitrogen
- 14 kg of phosphoric acid
From the percentages, we can express the total nitrogen and phosphoric acid from both fertilizers:
1. For nitrogen:
0.10x+0.05y≥14
Multiplying through by 100 to eliminate decimals:
10x+5y≥1400(Constraint 1)
2. For phosphoric acid:
0.06x+0.10y≥14
Again, multiplying through by 100:
6x+10y≥1400(Constraint 2)
Step 4: Set Up the Objective Function
The cost function to minimize is given by:
Z=6x+5y
Step 5: Solve the Constraints
We will rewrite the constraints in standard form:
1. 10x+5y≥1400
2. 6x+10y≥1400
Step 6: Find the Intercepts
To graph the constraints, we can find the intercepts for each equation.
For Constraint 1:
- Let x=0:
5y=1400⇒y=280(0,280)
- Let y=0:
10x=1400⇒x=140(140,0)
For Constraint 2:
- Let x=0:
10y=1400⇒y=140(0,140)
- Let y=0:
6x=1400⇒x=14006≈233.33(7003,0)
Step 7: Graph the Constraints
Plot the points (0,280), (140,0), (0,140), and (7003,0) on a graph. Draw the lines for each constraint and identify the feasible region.
Step 8: Identify Corner Points
The corner points of the feasible region will be where the constraints intersect. We can find the intersection points by solving the equations:
1. 10x+5y=1400
2. 6x+10y=1400
Step 9: Solve the System of Equations
From the first equation:
y=1400−10x5=280−2x
Substituting into the second equation:
6x+10(280−2x)=1400
6x+2800−20x=1400
−14x=−1400⇒x=100
Substituting x=100 back into y=280−2(100):
y=80
Step 10: Calculate the Minimum Cost
Now we can find the minimum cost using the values of x and y:
Z=6(100)+5(80)=600+400=1000
Final Answer
The farmer should use:
- 100 kg of fertilizer F1
- 80 kg of fertilizer F2
The minimum cost is Rs. 1000.
Let:
- x = amount (in kg) of fertilizer F1
- y = amount (in kg) of fertilizer F2
From the problem, we know:
- Fertilizer F1 contains:
- 10% nitrogen
- 6% phosphoric acid
- 5% nitrogen
- 10% phosphoric acid
The farmer needs at least:
- 14 kg of nitrogen
- 14 kg of phosphoric acid
1. For nitrogen:
0.10x+0.05y≥14
Multiplying through by 100 to eliminate decimals:
10x+5y≥1400(Constraint 1)
0.06x+0.10y≥14
Again, multiplying through by 100:
6x+10y≥1400(Constraint 2)
The cost function to minimize is given by:
Z=6x+5y
We will rewrite the constraints in standard form:
1. 10x+5y≥1400
2. 6x+10y≥1400
To graph the constraints, we can find the intercepts for each equation.
- Let x=0:
5y=1400⇒y=280(0,280)
- Let y=0:
10x=1400⇒x=140(140,0)
- Let x=0:
10y=1400⇒y=140(0,140)
- Let y=0:
6x=1400⇒x=14006≈233.33(7003,0)
Plot the points (0,280), (140,0), (0,140), and (7003,0) on a graph. Draw the lines for each constraint and identify the feasible region.
The corner points of the feasible region will be where the constraints intersect. We can find the intersection points by solving the equations:
1. 10x+5y=1400
2. 6x+10y=1400
From the first equation:
y=1400−10x5=280−2x
6x+10(280−2x)=1400
6x+2800−20x=1400
−14x=−1400⇒x=100
Substituting x=100 back into y=280−2(100):
y=80
Now we can find the minimum cost using the values of x and y:
Z=6(100)+5(80)=600+400=1000
The farmer should use:
- 100 kg of fertilizer F1
- 80 kg of fertilizer F2
Topper's Solved these Questions
Similar Questions
There are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs Rs. 10 per kg and ‘B’ cost Rs. 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirement are met at a minimum cost.
View SolutionA gardener has supply of fertilizer A which consists of 10% nitrogen and 6% phosphoric acid and fertilizer B which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If fertilizer A costs 10.60 per kg and fertilizer B costs 8.40 per kg, what is the minimum cost at which the farmer can meet the nutrient requirement by using a combination of both types of fertilizers?
View SolutionA farmer has a supply of chemical fertilizer of type. A which 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After soil test, it is found that at least 7kg of nitrogen and same quantity fo phosphoric acid is required for a good crop. The fertilizer of type A costs 5.00 per kg and the type B costs 8.00 per kg. Using Linear programming, find how many kilograms of each type of the fertilizer should be bought to meet the requirement and for the cost to be minimum. Find hte feasible region in the graph.
View SolutionA tea-shop owner mixes two kinds of tea, type A and type B, in the ratio 3:5. If type A costs Rs 200 per kg and type B costs Rs 160 per kg, find the price at which the blend must be sold to make a profit of 8%.
View SolutionA fruit grower canuse two types of fertilizer in his garden brand P and brand Q. The amounts (in kg) of nitrogen phosphoric acid, potash, and chlorine a bag of each brand are given in the stable. Tests indicate that the garden needs at least 240kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
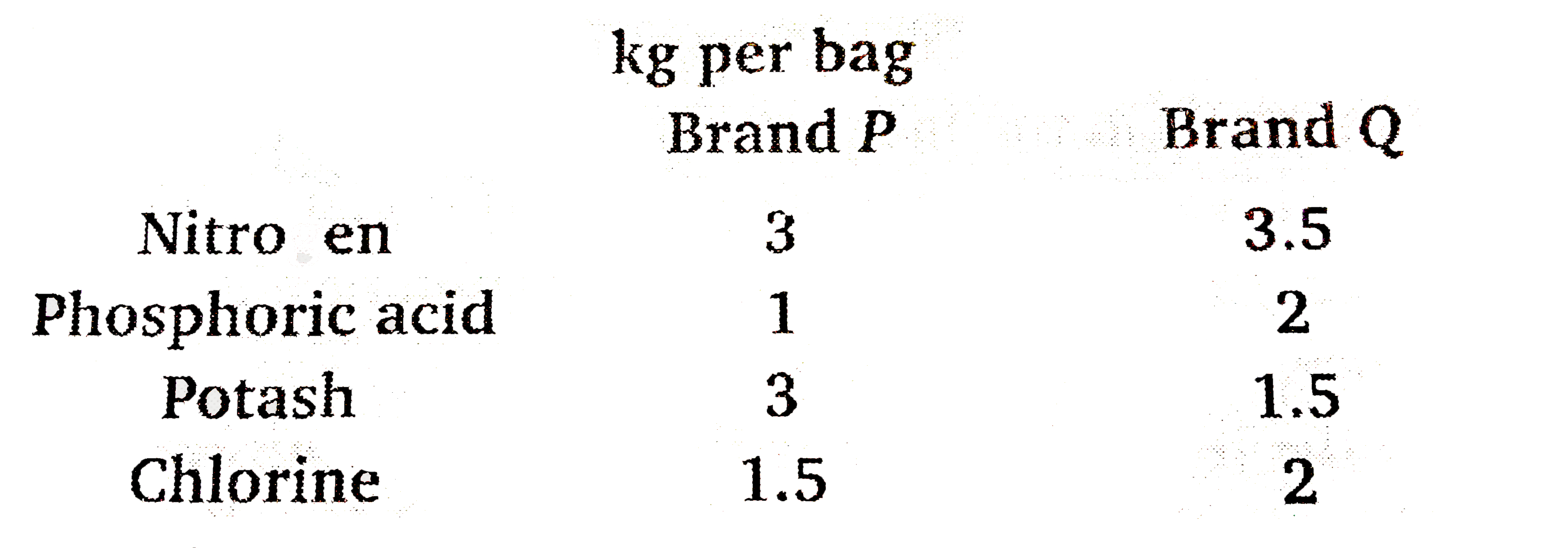
View SolutionFind the cost of 3(13) kg of rice at Rs40(12) per kg.
View SolutionA mixed grain flour is made by mixing 2 parts of mixed grains and three parts of wheat flour. If the mixed grains cost Rs 40 per kg and wheat costs Rs 30 per kg, find at what price the mixed grain flour needs to be sold to make a profit of 10%
View SolutionReaction of phosphoric acid with Ca5(PO4)3F yields a fertiliser 'triple superphosphate'. Represent the same through balanced chemical equations.
View SolutionIf 1 kg of common salt costs Rs. 7 and 1 kg of sugar costs Rs. 14.
What would be the cost of 1 mole of salt and sugar-
View SolutionA trader mixes two varieties of salt, viz. A and B. The cost price of A was Rs 28 per kg and of B was Rs 21 per kg. If he mixes these two varities in the ratio 2:5 , at what price per kg should he sell the mixture to make an profit of 5% ?
View Solution
