Question

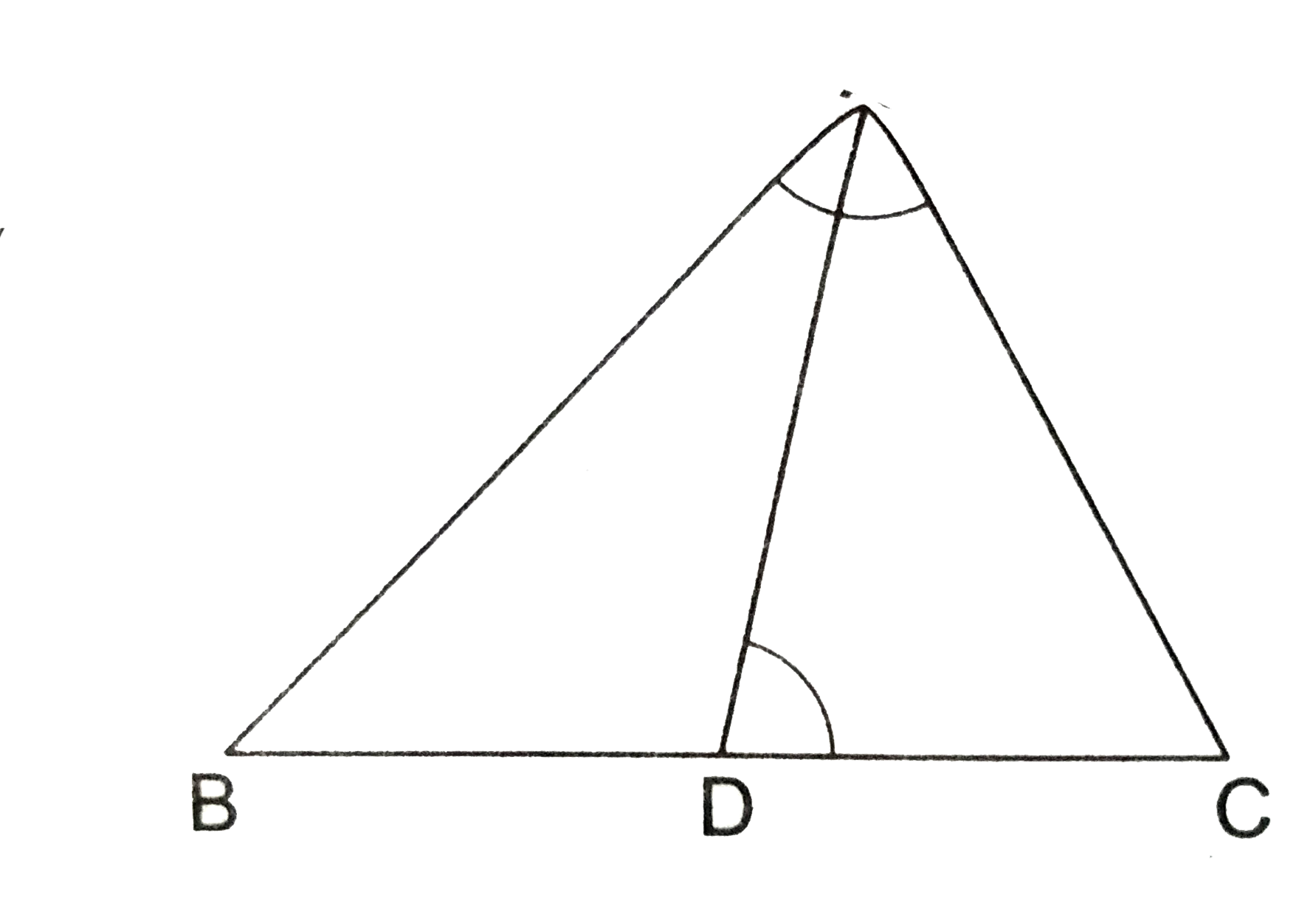
Let O be the in-centre of a triangle ABC and D be a point on the side BC of $\Delta ABC$, such that $OD\perp BC$ If $\angle BOD={15}^{\circ }$, then $\angle ABC=?$

Answer

`150^(@)`

Explanation

To solve the problem, we need to determine the angle ABC given the conditions provided. Let's break down the solution step by step.

1. Identify the Incenter and Given Angles:
- Let O be the incenter of triangle ABC.
- We know that OD is perpendicular to BC, which means angle ODB = 90°.
- We are given that angle BOD = 15°.

2. Calculate Angle AOD:
- In triangle BOD, we can find angle AOD using the fact that the sum of angles in a triangle is 180°.
- We have:
\( \text{Angle BOD} + \text{Angle ODB} + \text{Angle AOD} = 180° \)
- Substituting the known values:
\( 15° + 90° + \text{Angle AOD} = 180° \)
- Simplifying this gives:
\( \text{Angle AOD} = 180° - 105° = 75° \)

3. Relate Angle AOD to Angle ABC:
- Since O is the incenter, angle AOD is equal to half of angle ACB (because the angle bisector divides the angle into two equal parts).
- Therefore, we have:
\( \text{Angle ACB} = 2 \times \text{Angle AOD} = 2 \times 75° = 150° \)

4. Use the Triangle Angle Sum Property:
- In triangle ABC, the sum of the angles is 180°:
\( \text{Angle A} + \text{Angle B} + \text{Angle C} = 180° \)
- We know angle C (which is angle ACB) is 150°, so:
\( \text{Angle A} + \text{Angle B} + 150° = 180° \)
- This simplifies to:
\( \text{Angle A} + \text{Angle B} = 30° \)

5. Determine Angle ABC:
- Since angle A and angle B are supplementary to angle C, we can express angle B in terms of angle A:
\( \text{Angle B} = 30° - \text{Angle A} \)
- However, we need to find the specific value of angle ABC. We can assume that angle A is equal to angle B for simplicity in this case (as the problem does not specify otherwise).
- Thus, we can set:
\( 2 \times \text{Angle B} = 30° \)
- This gives:
\( \text{Angle B} = 15° \)

Final Answer:
Thus, the angle ABC is \( 15° \).