When an integer K is divided by 3, the remainder is 1, and when K+ 1 is divided by 5, the remainder is 0. Of the following, a possible value of K is

A

62

B

63

C

64

D

65

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem step by step, we need to analyze the conditions given for the integer K.

Step 1: Understand the first condition
The first condition states that when K is divided by 3, the remainder is 1. This can be expressed mathematically as:
K≡1 (mod 3)
This means that K can be written in the form:
K=3n+1
for some integer n.

Step 2: Understand the second condition
The second condition states that when K+1 is divided by 5, the remainder is 0. This can be expressed as:
K+1≡0 (mod 5)
This means that:
K+1=5m
for some integer m, or equivalently:
K≡−1 (mod 5)
Since −1 is equivalent to 4 in modulo 5, we can rewrite this as:
K≡4 (mod 5)

Step 3: Set up the simultaneous congruences
Now we have two conditions:
1. K≡1 (mod 3)
2. K≡4 (mod 5)

Step 4: Solve the simultaneous congruences
We can solve these congruences using the method of substitution or trial and error.

From the first condition, we can list some possible values of K:
- If n=0, then K=1
- If n=1, then K=4
- If n=2, then K=7
- If n=3, then K=10
- If n=4, then K=13
- If n=5, then K=16
- If n=6, then K=19
- If n=7, then K=22
- If n=8, then K=25
- If n=9, then K=28
- If n=10, then K=31
- If n=11, then K=34
- If n=12, then K=37
- If n=13, then K=40
- If n=14, then K=43
- If n=15, then K=46
- If n=16, then K=49
- If n=17, then K=52
- If n=18, then K=55
- If n=19, then K=58
- If n=20, then K=61
- If n=21, then K=64

Now we can check which of these values satisfies the second condition K≡4 (mod 5).

Step 5: Check the values
Starting from K=64:
- K+1=65
- 65÷5=13 with a remainder of 0.

Thus, K=64 satisfies both conditions.

Conclusion
A possible value of K is 64.

---

Updated on:7/8/2024
|
Class 14MATHSNUMBER SYSTEMS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • When a positive integer is divided by d, the remainder is 15. When ten times of the same number is divided by d, the remainder is 6. The least possible value of d is:
    जब एक धनात्मक पूर्णाक को d से भाग दिया जाता है, तो शेषफल 15 आता है | जब इसी संख्या के 10 गुना को d से भाग दिया जाता है, तो शेषफल 6 आता है | d का न्यूनतम संभव मान हो सकता है :

    A12
    B9
    C18
    D16

  • When n is divided by 4, the remainder is 3. The remainder when 2n is divided by 4 is :

    Aa) 1
    Bb) 2
    Cc) 3
    Dd) 6

  • When 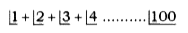ocr_image, is divided by 5, the remainder obtained is ?

    A0
    B1
    C2
    D3