In a ΔABC .G is centroid AG = BC find angle BGC
The correct Answer is:∠BGC=90∘
To solve the problem, we need to find the angle BGC in triangle ABC where G is the centroid and AG=BC.
1. Draw Triangle ABC:
Start by sketching triangle ABC with points A, B, and C.
2. Identify the Centroid G:
The centroid G of triangle ABC is the point where the three medians intersect. A median is a line segment from a vertex to the midpoint of the opposite side.
3. Label the Sides:
Given that AG=BC, we can denote BC=2X for some value X. Therefore, AG=2X.
4. Determine the Segments:
Since G is the centroid, it divides the median AG in the ratio 2:1. This means:
- AG=2X
- GD=X (where D is the midpoint of BC)
5. Establish Angles:
In triangle BGC, since BG=GC (as G is the centroid and divides BC into two equal parts), we can denote the angles at B and C as α and β respectively.
6. Use the Isosceles Triangle Property:
Since BG=GC, angles ∠BGC and ∠GBC are equal. Thus, we can say:
∠BGC=∠GBC=α
and ∠BCG=β.
7. Apply the Triangle Sum Theorem:
The sum of angles in triangle BGC is 180∘:
α+α+β=180∘
Simplifying gives:
2α+β=180∘
8. Relate Angles:
Since AG=BC and we have established the segments, we can conclude that α+β=90∘ (from the properties of the triangle).
9. Final Calculation:
Substituting β=90∘−α into the equation 2α+β=180∘:
2α+(90∘−α)=180∘
This simplifies to:
α+90∘=180∘
Therefore,
α=90∘−β
Thus, ∠BGC=90∘.
Conclusion:
The angle BGC is 90∘.
Start by sketching triangle ABC with points A, B, and C.
The centroid G of triangle ABC is the point where the three medians intersect. A median is a line segment from a vertex to the midpoint of the opposite side.
Given that AG=BC, we can denote BC=2X for some value X. Therefore, AG=2X.
Since G is the centroid, it divides the median AG in the ratio 2:1. This means:
- AG=2X
- GD=X (where D is the midpoint of BC)
In triangle BGC, since BG=GC (as G is the centroid and divides BC into two equal parts), we can denote the angles at B and C as α and β respectively.
Since BG=GC, angles ∠BGC and ∠GBC are equal. Thus, we can say:
∠BGC=∠GBC=α
and ∠BCG=β.
The sum of angles in triangle BGC is 180∘:
α+α+β=180∘
Simplifying gives:
2α+β=180∘
Since AG=BC and we have established the segments, we can conclude that α+β=90∘ (from the properties of the triangle).
Substituting β=90∘−α into the equation 2α+β=180∘:
2α+(90∘−α)=180∘
This simplifies to:
α+90∘=180∘
Therefore,
α=90∘−β
Thus, ∠BGC=90∘.
The angle BGC is 90∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
A12B16C24D8 - Question 2 - Select One
Suppose z1,z2,z3 represent the vertices A, B and C respectively of a ΔABC with centroid at G. If the mid point of AG is the origin, then
Az1+z2+z3=0B2z1+z2+z3=0Cz1+z2+4z3=0D4z1+z2+z3=0 - Question 3 - Select One
In ABC, G is the centroid, AB = 15 cm, BC = 18 cm and AC = 25 cm. Find GD, where D is the mid-point of BC.
A13√86 cmB23√86 cmC83√15Dnone of these
In ΔABC,AD=BC. Find x.
View SolutionIn ΔABC,AD=BC. Find x.
View Solution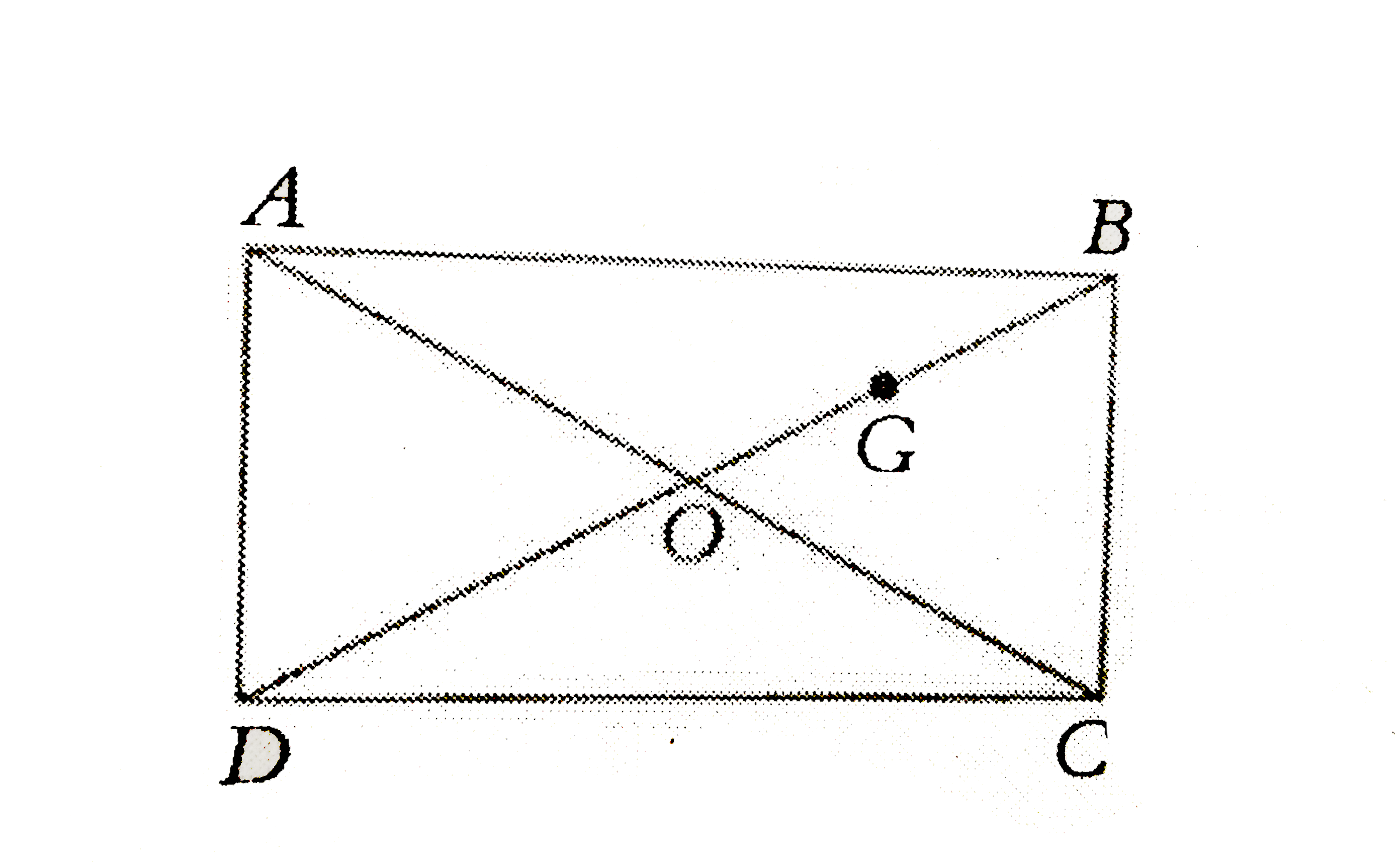
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC . If BG=4 cm, then find the length of AC.View Solution
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC. If BG=4cm, then find the length of AC.View SolutionIn ABC, G is the centroid, AB = 15 cm, BC = 18 cm and AC = 25 cm. Find GD, where D is the mid-point of BC.
View Solution

