A pilot does not fall down when his aeroplane loops the loop. Why ?
To understand why a pilot does not fall down when his aeroplane loops the loop, we need to analyze the forces acting on the pilot at the highest point of the loop.
1. Identify the Forces Acting on the Pilot:
At the highest point of the loop, two main forces act on the pilot:
- The gravitational force (weight) acting downwards, which is given by mg, where m is the mass of the pilot and g is the acceleration due to gravity.
- The normal force (N) exerted by the seat of the aeroplane acting upwards.
2. Understand the Requirement for Circular Motion:
For the pilot to remain in circular motion at the highest point of the loop, there must be a net centripetal force directed towards the center of the loop. This centripetal force (Fc) is provided by the difference between the gravitational force and the normal force:
Fc=mg−N
This centripetal force must also equal the required centripetal force for circular motion, which is given by:
Fc=mv2R
where v is the velocity of the aeroplane at the highest point, and R is the radius of the loop.
3. Set Up the Equation:
By equating the two expressions for centripetal force, we get:
mg−N=mv2R
4. Condition for the Pilot Not to Fall:
For the pilot not to fall, the normal force N must be greater than or equal to zero:
N≥0
Substituting N from the centripetal force equation gives:
mg−mv2R≥0
Rearranging this leads to:
mg≥mv2R
5. Derive the Maximum Velocity:
Dividing both sides by m (assuming m≠0):
g≥v2R
Rearranging gives:
v2≤gR
Taking the square root of both sides, we find:
v≤√gR
This indicates that there is a maximum velocity at the highest point of the loop for the pilot to remain safely in the seat.
6. Conclusion:
Thus, as long as the velocity of the aeroplane at the highest point of the loop is less than or equal to √gR, the pilot will not fall down because the gravitational force will provide enough centripetal force to keep him in circular motion.
At the highest point of the loop, two main forces act on the pilot:
- The gravitational force (weight) acting downwards, which is given by mg, where m is the mass of the pilot and g is the acceleration due to gravity.
- The normal force (N) exerted by the seat of the aeroplane acting upwards.
For the pilot to remain in circular motion at the highest point of the loop, there must be a net centripetal force directed towards the center of the loop. This centripetal force (Fc) is provided by the difference between the gravitational force and the normal force:
Fc=mg−N
This centripetal force must also equal the required centripetal force for circular motion, which is given by:
Fc=mv2R
where v is the velocity of the aeroplane at the highest point, and R is the radius of the loop.
By equating the two expressions for centripetal force, we get:
mg−N=mv2R
For the pilot not to fall, the normal force N must be greater than or equal to zero:
N≥0
Substituting N from the centripetal force equation gives:
mg−mv2R≥0
Rearranging this leads to:
mg≥mv2R
Dividing both sides by m (assuming m≠0):
g≥v2R
Rearranging gives:
v2≤gR
Taking the square root of both sides, we find:
v≤√gR
This indicates that there is a maximum velocity at the highest point of the loop for the pilot to remain safely in the seat.
Thus, as long as the velocity of the aeroplane at the highest point of the loop is less than or equal to √gR, the pilot will not fall down because the gravitational force will provide enough centripetal force to keep him in circular motion.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM ANGULAR VELOCITY)
Explore 4 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM CENTRIPETAL FORCE)
Explore 31 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (SHORT ANSWER QUESTIONS)
Explore 33 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
You may have seen in a circus a motorcyclist driving in vertical loops inside a death well (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point of death well with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m ?
View SolutionYou may have seen in a circus a motorcyclist driving in a vertical loop inside a 'death well' chamber with holes, so the spectators can watch from outside. Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required to perform a vertical loop if the radius of the chamber is 25 m ?
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionMagnetic lines form continuous closed loop. Why ?
View SolutionA: The magnetic moment of a current carrying planar loop does depend on the space of the loop.
R: The magnetic moemnt is a vector quantity.
View SolutionA uniform circular loop of radius a and resistance R is pulled at a constant velocity v out of a region of a uniform plane of the loop and the velocity are both perpendicular to B. Then the electrical power in the circular loop at the instant when the arc (of the circular loop) outside the region of magnetic field subtends an angle π3 at the centre of the loop is
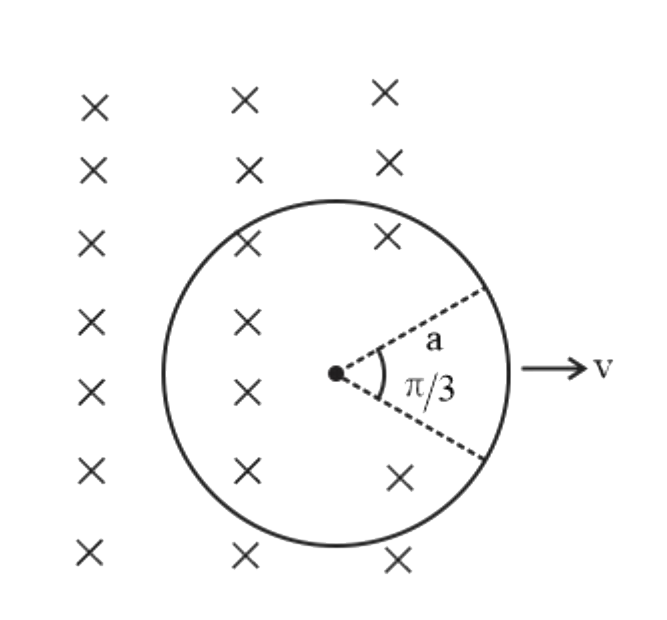
View Solution(a) A closed loop is held stationary in the magnetic field between the north and south poles of two permanent magnets held fixed. Can we hope to generate current in the loop by using very strong magnets?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor. Is a current induced in the loop (i) when it is wholly inside the region between the capacitor plates (ii) when it is partially outside the plates of the capacitor? The electric field is normal to the plane of the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field region (Fig. 6.8) to a field-free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops.

(d) Predict the polarity of the capacitor in the situation described by Fig. 6.9.

View SolutionA particle of mass m is released from point A as shown in the gigure. Would it loop the loop if H=4r? What is the force on the circular track when it is at point (a) B, (b) C?

View SolutionWhy does the nose of some people start bleeding when an aeroplane climbs up suddenly?
View SolutionWhy earth does not fall towards sun due to its attrraction?
View Solution
