The vacuum kept in between the walls of a thermos flask reduces the heat transfer by :
conduction only
convection only
radiation only
conduction and convection.
The correct Answer is:D
Step by step video, text & image solution for The vacuum kept in between the walls of a thermos flask reduces the heat transfer by : by Physics experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - HEATEXERCISE - TEST YOURSELF (SHORT/LONG ANSWER TYPE QUESTIONS)56videos
HEAT
- BOOK - ICSECHAPTER - HEATEXERCISE - TEST YOURSELF (NUMERICALS )7videos
HEAT
- BOOK - ICSECHAPTER - HEATEXERCISE - TEST YOURSELF (MATCH THE COLUMN)1videos
HEAT
- BOOK - ICSECHAPTER - FORCE AND PRESSURE : MOTION EXERCISE - EXERCISES (SECTION II) (Picture Study)4videos
FORCE AND PRESSURE : MOTION
- BOOK - ICSECHAPTER - LIGHT ENERGYEXERCISE - EXERCISE (PICTURE STUDY)10videos
LIGHT ENERGY
Similar Questions
Air is bad conductor of heat or partly conducts heat, still vacuum is to be placed between the walls of the thermos flask because
View SolutionLook at the picture of the thermos flask and answer the following question
The outer surface of the inner wall of a thermos flask has a very shiny surface. What effect will this have on heat escaping from a hot liquid inside a thermos flask?View SolutionTea placed in thermos flask is an example of
View SolutionExplain briefly the process of heat transfer by radiation.
View SolutionLook at the picture of the thermos flask and answer the following question
Which means of heat transfer are prevented by having a vacuum between the two walls of thermos flasks?View SolutionGive one example of heat transfer by radiation.
View Solution
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal toView Solution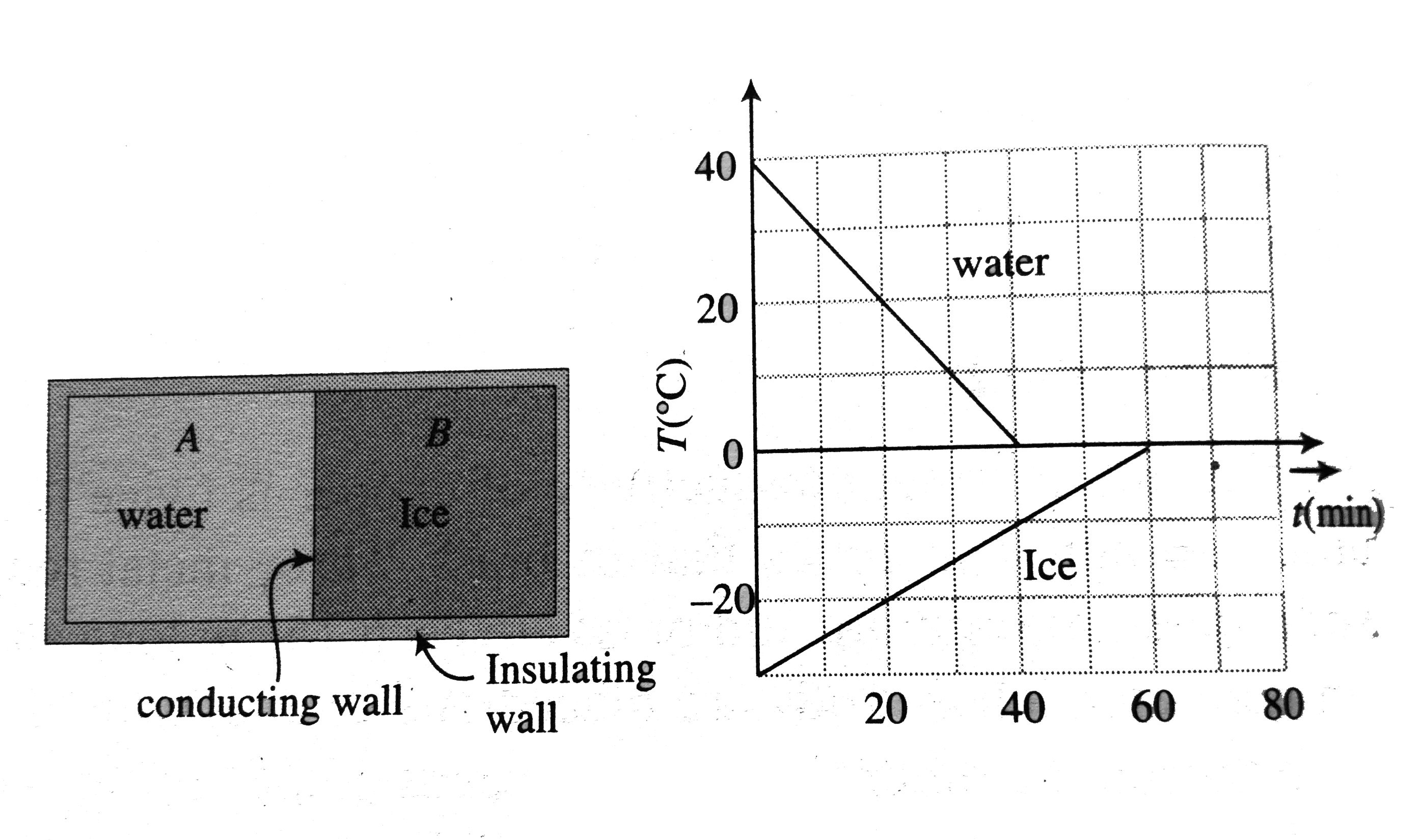
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
The value of rate P is?View Solution-
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.
Initial mass of the ice in the container equal toView Solution -
A 0.60 kg sample of water and a sample of ice are placed in two compartmetnts A and B separated by a conducting wall, in a thermally insulated container. The rate of heat transfer from the water to the ice through the conducting wall is constant P, until thermal equilibrium is reached. The temperature T of the liquid water and the ice are given in graph as functions of time t. Temperature of the compartments remain homogeneous during whole heat transfer process. Given specific heat of ice =2100J/kg−K, specific heat of water =4200J/kg−K, and latent heat of fusion of ice =3.3×105J/kg.View Solution