A force of 15 N is required to pull up a body of mass 2 kg through a distance 5 m along an inclined plane making an angle of 30∘ with horizontal as shown in fig calculate :
(i)the work done by the force in pulling the body.
(ii)The force due to gravity on the body,
(iii)the work done against by the force due to gravity Take :g=9.8 m s−2.
(iv)Account for the difference in answers of part (i) and part (iii).
To solve the given problem step by step, we will address each part of the question systematically.
Given Data:
- Force required to pull the body, F=15N
- Mass of the body, m=2kg
- Distance along the inclined plane, d=5m
- Angle of inclination, θ=30∘
- Acceleration due to gravity, g=9.8m/s2
(i) Work Done by the Force in Pulling the Body
The work done W by a force is calculated using the formula:
W=F⋅d⋅cos(ϕ)
where ϕ is the angle between the force and the direction of displacement. Since the force is applied in the direction of displacement along the incline, ϕ=0∘ and cos(0)=1.
Substituting the values:
W=15N⋅5m⋅1=75J
(ii) Force Due to Gravity on the Body
The force due to gravity Fg acting on the body can be calculated using:
Fg=m⋅g
Substituting the values:
Fg=2kg⋅9.8m/s2=19.6N
(iii) Work Done Against the Force Due to Gravity
To find the work done against gravity while moving the body up the incline, we need to consider the component of gravitational force acting along the incline. This component is given by:
Fg,along=Fg⋅sin(θ)
Now substituting the values:
Fg,along=19.6N⋅sin(30∘)=19.6N⋅12=9.8N
Now, the work done against gravity Wg is:
Wg=Fg,along⋅d
Substituting the values:
Wg=9.8N⋅5m=49J
(iv) Account for the Difference in Answers of Part (i) and Part (iii)
Now we need to find the difference between the work done by the applied force and the work done against gravity:
Difference=W−Wg=75J−49J=26J
Explanation: The difference of 26J can be attributed to the work done against friction or other opposing forces that may be present while pulling the body up the incline. The applied force of 15N does not only work against gravity but also overcomes additional resistive forces.
Summary of Answers:
- (i) Work done by the force: 75 J
- (ii) Force due to gravity on the body: 19.6 N
- (iii) Work done against the force due to gravity: 49 J
- (iv) The difference is due to work done against friction or other resistive forces: 26 J
- Force required to pull the body, F=15N
- Mass of the body, m=2kg
- Distance along the inclined plane, d=5m
- Angle of inclination, θ=30∘
- Acceleration due to gravity, g=9.8m/s2
W=F⋅d⋅cos(ϕ)
where ϕ is the angle between the force and the direction of displacement. Since the force is applied in the direction of displacement along the incline, ϕ=0∘ and cos(0)=1.
W=15N⋅5m⋅1=75J
Fg=m⋅g
Substituting the values:
Fg=2kg⋅9.8m/s2=19.6N
Fg,along=Fg⋅sin(θ)
Now substituting the values:
Fg,along=19.6N⋅sin(30∘)=19.6N⋅12=9.8N
Wg=Fg,along⋅d
Substituting the values:
Wg=9.8N⋅5m=49J
Difference=W−Wg=75J−49J=26J
- (i) Work done by the force: 75 J
- (ii) Force due to gravity on the body: 19.6 N
- (iii) Work done against the force due to gravity: 49 J
- (iv) The difference is due to work done against friction or other resistive forces: 26 J
Topper's Solved these Questions
- WORK ENERGY AND POWERBOOK - ICSECHAPTER - WORK ENERGY AND POWEREXERCISE - EXERCISE-2(A)
31 Videos
- WORK ENERGY AND POWERBOOK - ICSECHAPTER - WORK ENERGY AND POWEREXERCISE - EXERCISE-2(A) (MULTIPLE CHOICE TYPE )
2 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
Similar Questions
The work done by the force of gravity is 100 J

View SolutionWhen a body is thrown up , work done by gravity on the body is
View SolutionThe relationship between force and position is shown in fig ( in one dimensional case). The work done in displacing a body from x=1cm to x = 5 cm is:
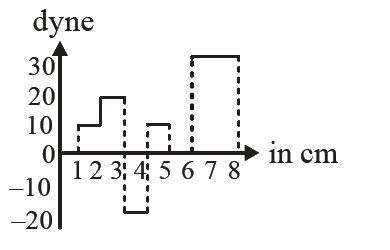
View SolutionThe work done by a body is the product of force and
View SolutionA person pushes a block of mass 4 kg up a frictionless inclined plane 10 m long and that makes an angle of 30∘ with the horizontal . Then the work done is
View SolutionWhen work done by force of gravity is negative, then
View SolutionA man pulls a box on a horizontal floor through a distance of 20 m with a force of 30 N applied along a rope tied to the box and making and angle of 60° with the horizontal. Calculate the work done.
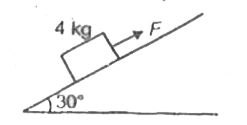
View SolutionA block of mass 4 kg is pulled along a smooth inclined plane of inclination 30∘ with constant velocity 3 m/s as shown, power delivered by the force is
View SolutionA body, acted upon by a force of 50N, is displaced through a distance 10m in direction making an angle of 60∘ with the force. Find the work done by the force.
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30° with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. Find the least force required to pull the body up the plane.
View Solution
