How is the refractive index of a medium related to the real and apparent depths of an object in that medium ?
To understand the relationship between the refractive index of a medium and the real and apparent depths of an object submerged in that medium, we can follow these steps:
1. Define Refractive Index:
The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in the medium (v). Mathematically, it is expressed as:
μ=cv
2. Understanding Real Depth:
The real depth is the actual distance of an object from the surface of the medium to the object itself. For example, if a coin is placed at the bottom of a beaker filled with liquid, the real depth (h) is the distance from the surface of the liquid to the coin.
3. Understanding Apparent Depth:
The apparent depth is the depth at which the object appears to be when viewed from above the surface of the liquid. Due to the refraction of light, the coin will appear to be at a different height (h') than its actual position.
4. Establishing the Relationship:
The relationship between the refractive index (μ), real depth (h), and apparent depth (h') can be expressed by the formula:
μ=Real Depth (h)Apparent Depth (h')
5. Conclusion:
This means that the refractive index of the medium is directly proportional to the ratio of the real depth to the apparent depth. If the refractive index is known, one can determine either the real or apparent depth if the other is known.
Summary:
The refractive index (μ) of a medium relates to the real depth (h) and the apparent depth (h') of an object submerged in that medium by the formula:
μ=hh′
The refractive index (μ) of a medium is defined as the ratio of the speed of light in vacuum (c) to the speed of light in the medium (v). Mathematically, it is expressed as:
μ=cv
The real depth is the actual distance of an object from the surface of the medium to the object itself. For example, if a coin is placed at the bottom of a beaker filled with liquid, the real depth (h) is the distance from the surface of the liquid to the coin.
The apparent depth is the depth at which the object appears to be when viewed from above the surface of the liquid. Due to the refraction of light, the coin will appear to be at a different height (h') than its actual position.
The relationship between the refractive index (μ), real depth (h), and apparent depth (h') can be expressed by the formula:
μ=Real Depth (h)Apparent Depth (h')
This means that the refractive index of the medium is directly proportional to the ratio of the real depth to the apparent depth. If the refractive index is known, one can determine either the real or apparent depth if the other is known.
The refractive index (μ) of a medium relates to the real depth (h) and the apparent depth (h') of an object submerged in that medium by the formula:
μ=hh′
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) MULTIPLE CHOICE TYPE
2 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(C) NUMERICALS
3 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBOOK - ICSECHAPTER - REFRACTION OF LIGHT AT PLANE SURFACESEXERCISE - EXERCISE-4(B) NUMERICALS
2 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
- REFRACTION THROUGH A LENS BOOK - ICSECHAPTER - REFRACTION THROUGH A LENS EXERCISE - EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
2 Videos
Similar Questions
Define refractive index of a medium.
View SolutionRefractive index of a medium depends on
View SolutionHow does the refractive index of a medium depend on its temperature ?
View SolutionThe apparent depth of an object O from AB is
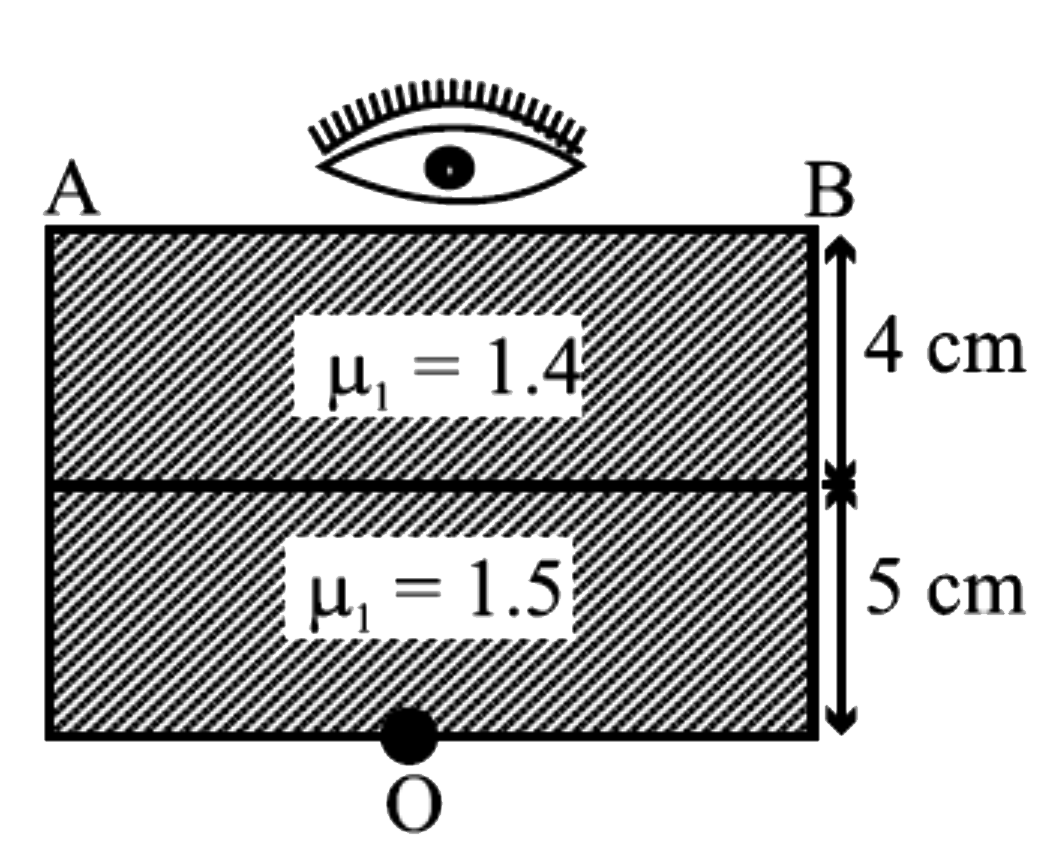
View SolutionHow is the refractive index of a medium related to the speed of light ? Obtain an expression for refractive index of a medium with respect to another in terms of speed of light in these two media ?
View SolutionHow does the refractive index of a medium depend on the wavelength of light used ?
View Solution(a) Compare the speed of light of wavelength 4000 Å (i.e., violet light) and 8000 Å (i.e. red light) in vacuum.
(b) How is the refractive index of a medium related to the speed of light in it and in vacuum or air ?
View SolutionHow is it related to the refractive index of the medium ?
View SolutionDefine the term refractive index of a medium. Can it be less than 1 ?
View SolutionWhen light is refracted into a medium
View Solution
