∫π20cos2xdx ਸੀਮਿਤ ਇਨਟਿਗਰਲਾਂ ਦੇ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਦਿੱਤੇ ਹੋਏ ਫਲਨ ਵਿੱਚ ਇਨਟਿਗਰਲ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ।
Step by step video & image solution for int_0^(pi/2) cos^2x dx ਸੀਮਿਤ ਇਨਟਿਗਰਲਾਂ ਦੇ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ ਦਿੱਤੇ ਹੋਏ ਫਲਨ ਵਿੱਚ ਇਨਟਿਗਰਲ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ਦਿੱਤੇ ਫਲਨ ਦਾ ਐਂਟੀ ਡੈਰੀਵੇਟਿਵ ਇਨਟਿਗਰਲ ਨਿਰੀਖਣ ਵਿਧੀ ਦੁਆਰਾ ਪਤਾ ਕਰੋ : Sin(2x)
View Solutionਵਕਰ y=x, ਰੇਖਾਵਾਂ x=1,x=4 ਅਤੇ x-ਧੁਰੇ ਨਾਲ ਘਿਰੇ ਖੇਤਰ ਦਾ ਪਹਿਲੀ ਚੌਥਾਈ ਵਿੱਚ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ।
View SolutionEvaluate: ∫π/20cos2x dx
View SolutionEvaluate ∫π20cos2xdx
View Solution∫π0(cos2x)dx,
View Solution(i) ∫π/20cosxdx (ii) ∫π/2−π/2cosxdx (iii) ∫π/20cos2xdx
View Solutionu=∫π20cos(2π3sin2x)dx and v=∫π20cos(π3sinx)dx
View SolutionI1=∫π40sin2xdx এবং I2=∫π40cos2xdx হলে
View Solution(x+1)n ਦੇ ਪ੍ਰਸਾਰ ਵਿੱਚ (r−1)ਵੇਂ, rਵੇਂ ਅਤੇ (r+1)ਵੇਂ ਪਦਾਂ ਦੇ ਗੁਣਾਂਕਾਂ ਦਾ ਅਨੁਪਾਤ 1:3:5 ਹੈ, n ਅਤੇ r ਪਤਾ ਕਰੋ।
View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ P(A)=12,P(A∪B)=35 ਅਤੇ P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਆਪਸ ਵਿੱਚ ਨਿਵੇਕਲੀਆਂ ਹਨ
View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ P(A)=12,P(A∪B)=35 ਅਤੇ P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਅਜ਼ਾਦ ਹਨ।
View Solutionਇੱਕ ਪੈਡਸਟਲ ਦੇ ਸਿਖ਼ਰ 'ਤੇ ਇਕ 1.6mਉੱਚੀਮੂਰਤੀਲੱਗੀਹੋਈਹੈ।ਜ਼ਮੀਨਦੇਇੱਕਬਿੰਦੂਤੋਂਮੂਰਤੀਦੇਸਿਖ਼ਰਦਾਉੱਚਾਣਕੋਣ60^@ਹੈਅਤੇਇਸਹੀਬਿੰਦੂਤੋਂਪੈਡਸਟਲਦੇਸਿਖਰਦਾਉੱਚਾਣਕੋਣ45^@ ਹੈ।ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ।
View Solutionਇੱਕ ਨਦੀ ਦੇ ਪੂਲ ਦੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਨਦੀ ਦੇ ਸਨਮੁੱਖ ਕਿਨਾਰਿਆਂ ਦੇ ਨੀਵਾਨ ਕੋਣ 30∘ ਅਤੇ45∘ ਹੈ। ਜੇਕਰ ਪੂਲ, ਕਿਨਾਰਿਆਂ ਤੋਂ 3 m ਦੀ ਉੱਚਾਈ ਤੇ ਹੋਵੇ ਤਾਂ ਨਦੀ ਦੀ ਚੰੜਾਈ ਪਤਾ ਕਰੋ।
View Solutionਇਕ ਪਰਿਵਾਰ ਨੇ ਜਿਸ ਦੀ ਮਹੀਨੇਵਾਰ ਆਮਦਨ 20000 ਰੁਪਏ ਹੈ, ਭਿਨ-ਭਿਨ ਮੱਦਾਂ ਤੇ ਹਰ ਮਹੀਨੇ ਹੋਣ ਵਾਲੇ ਖਰਚ ਦੀ ਯੋਜਨਾ ਬਣਾਈ ਸੀ:-
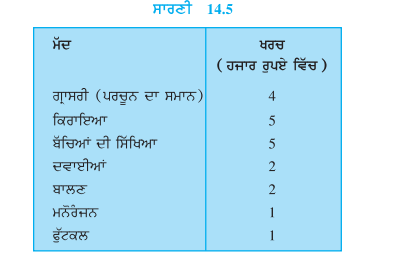 ਉੱਪਰ ਦਿੱਤੇ ਅਕੜਿਆਂ ਦਾ ਵਿਕ ਛੜ ਗ੍ਰਾਫ਼ ਬਣਾਓ।
ਉੱਪਰ ਦਿੱਤੇ ਅਕੜਿਆਂ ਦਾ ਵਿਕ ਛੜ ਗ੍ਰਾਫ਼ ਬਣਾਓ।
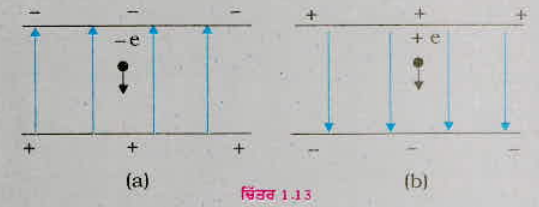
View Solutionਕੋਈ ਇਲੈਕਟ੍ਰਾਨ 2.0 x 10^ 4 N C^-1 ਪਰਿਮਾਣ ਦੇ ਇੱਕ ਸਮਾਨ ਬਿਜਲਈ ਖੇਤਰ ਵਿੱਚ 1.5cm ਦੂਰੀ ਤੱਕ ਡਿਗਦਾ ਹੈ। ਖੇਤਰ ਦਾ ਪਰਿਮਾਣ ਸਮਾਨ ਰਖਦੇ ਹੋਏ ਇਸਦੀ ਦਿਸ਼ਾ ਪਲਟ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ਅਤੇ ਹੁਣ ਕੋਈ ਹੋਰ ਪ੍ਰੋਟਾਨ ਇਸ ਖੇਤਰ ਵਿਚ ਉੱਨੀ ਹੀ ਦੂਰੀ ਤੱਕ ਡਿਗਦਾ ਹੈ ਦੋਵੇ ਕੇਸਾਂ ਵਿੱਚ ਡਿੱਗਨ ਵਿੱਚ ਲੱਗੇ ਸਮੇਂ ਦੀ ਗਣਨਾ ਕਰੋ। ਇਸ ਪਰਿਸਥਿਤੀ ਦੀ ਗੁਰੂਤਾ ਦੇ ਅਧੀਨ ਮੁਕਤ ਪਤਨ ਨਾਲ ਤੁਲਨਾ ਕਰੋ।
View SolutionSuppose I1=∫π20cos(πsin2x)dxandI2=∫π20cos(2πsin2x)dxandI3=∫π20cos(πsinx)dx, then
View Solution
