PQR ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ Pਸਮਕੋਣ ਹੈ ਅਤੇ QR 'ਤੇ ਬਿੰਦੂ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ PM⊥QR ਹੈ।ਦਰਸਾਉ ਕਿ PM2=QM.MR ਹੈ।
Step by step video & image solution for PQR ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦਾ ਕੋਣ Pਸਮਕੋਣ ਹੈ ਅਤੇ QR 'ਤੇ ਬਿੰਦੂ M ਇਸ ਤਰ੍ਹਾਂ ਸਥਿਤ ਹੈ ਕਿ PM bot QR ਹੈ।ਦਰਸਾਉ ਕਿ PM^2=QM.MR ਹੈ। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
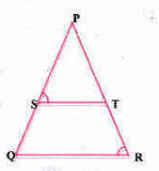
ਚਿੱਤਰ 6.16 ਵਿੱਚ PSsQ=PTTR ਹੈ ਅਤੇ ∠PST=∠PRQ ਹੈ। ਸਿੱਧ ਕਰੋ ਕਿ ΔPQR ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ।
View Solutionਜੇਕਰ tanA=43, ਤਾਂ ਕੋਣ A ਦੇ ਬਾਕੀ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ।
View Solutionਜਾਂਚ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੀਕਰਣਾਂ ਦੋ ਘਾਤੀ ਹਨ ਜਾਂ ਨਹੀ : (x+1)2=2(x−3)
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR . Show that PM2=QM.MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2=QM.MR .
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR . Show that PM2 = QM .MR.
View SolutionPQR is a Deltaright angled at P and M is a point on QR such that PM⊥QR. Show that PM2=QM⋅MR.
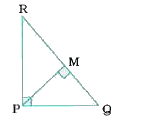
View Solutionਹੇਠ ਲਿਖੇ ਕਥਨ ਵਿਚ ਆਉਣ ਵਾਲੀ ਸੰਖਿਆਵਾਂ ਨੂੰ ਮਿਆਰੀ ਰੂਪ ਵਿਚ ਲਿਖੋ:- ਧਰਤੀ 'ਤੇ 1,353,000,000 ਕਿ.ਮੀ..^3 ਸਮੁੰਦਰੀ ਪਾਣੀ ਹੈ।
View Solutionਮੰਨ ਲਓ ਕਿ XY- ਤਲ ਵਿੱਚ ਸਥਿਤ ਸਾਰੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਸਮੂਹ L ਹੈ ਅਤੇ L ਵਿੱਚ R={(L1,L2):L1 ਸਮਾਂਤਰ ਹੈ L2ਨਾਲ}ਰਾਹੀਂਪਰਿਭਾਸ਼ਿਤਸੰਬੰਧRਹੈ।ਸਿੱਧਕਰੋਕਿRਇੱਕਸਮਤੁੱਲਸੰਬੰਧਹੈ।ਰੇਖਾy = 2x + 4 ਨਾਲ ਸੰਬੰਧਿਤ ਸਾਰੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਸਮੂਹ ਪਤਾ ਕਰੋ।
View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਹੇਠਾਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ f:N→N , ਇੱਕ-ਇੱਕ ਅਤੇ ਔਨਟੂ ਹੈ: f(x)={x+1ਜੇਕਰxਟਾਂਕਹੈx−1ਜੇਕਰxਜਿਸਤਹੈ
View SolutionAssume that all n in N For, f(n) = {((n+1)/2,,ਜੇਕਰ n ਟਾਂਕ ਹੈ,,),(n/2,,ਜੇਕਰ n ਜਿਸਤ ਹੈ,,):} A function defined by f:NrarrN Is Explain whether the function f is an onto. Also, verify your answer.
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM⊥QR. Show that PM2=QM.MR.
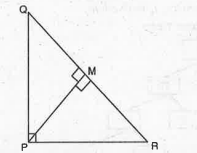
View SolutionPQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM.MR.
View Solution