ਇੱਕ ਪਿੱਗੀ ਬੈਂਕ ਵਿੱਚ, 50 ਪੈਸੇ ਦੇ ਸੌ ਸਿੱਕੇ ਹਨ, ₹1 ਦੇ ਪੰਜਾਹ ਸਿੱਕੇ ਹਨ, ₹ 2 ਦੇ ਵੀਹ ਸਿੱਕੇ ਅਤੇ ₹5 ਦੇ ਦਸ ਸਿੱਕੇ ਹਨ। ਜੇਕਰ ਪਿੱਗੀ ਬੈਂਕ ਨੂੰ ਹਿਲਾ ਕੇ ਉਲਟਾ ਕਰਨ ਤੇ ਕੋਈ ਇੱਕ ਸਿੱਕਾ ਬਾਹਰ ਡਿੱਗਣ ਦੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ (ਬਰਾਬਰ ਦੀ ਸੰਭਾਵਨਾ ਵਾਲੇ) ਤਾਂ ਉਸਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ਕਿ ਉਹ ਡਿੱਗਿਆ ਹੋਇਆ ਸਿੱਕਾ (1) 50 ਪੈਸੇ ਦਾ ਹੋਵੇਗਾ (2) ₹5 ਦਾ ਨਹੀਂ ਹੋਵੇਗਾ?
Step by step video & image solution for ਇੱਕ ਪਿੱਗੀ ਬੈਂਕ ਵਿੱਚ, 50 ਪੈਸੇ ਦੇ ਸੌ ਸਿੱਕੇ ਹਨ, ₹1 ਦੇ ਪੰਜਾਹ ਸਿੱਕੇ ਹਨ, ₹ 2 ਦੇ ਵੀਹ ਸਿੱਕੇ ਅਤੇ ₹5 ਦੇ ਦਸ ਸਿੱਕੇ ਹਨ। ਜੇਕਰ ਪਿੱਗੀ ਬੈਂਕ ਨੂੰ ਹਿਲਾ ਕੇ ਉਲਟਾ ਕਰਨ ਤੇ ਕੋਈ ਇੱਕ ਸਿੱਕਾ ਬਾਹਰ ਡਿੱਗਣ ਦੇ ਪਰਿਣਾਮ ਸਮਸੰਭਾਵੀ ਹਨ (ਬਰਾਬਰ ਦੀ ਸੰਭਾਵਨਾ ਵਾਲੇ) ਤਾਂ ਉਸਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ਕਿ ਉਹ ਡਿੱਗਿਆ ਹੋਇਆ ਸਿੱਕਾ (1) 50 ਪੈਸੇ ਦਾ ਹੋਵੇਗਾ (2) ₹5 ਦਾ ਨਹੀਂ ਹੋਵੇਗਾ? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ਇੱਕ ਚਿੱਤ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ, ਜਦੋਂ ਇੱਕ ਸਿੱਕੇ ਨੂੰ ਇਕ ਵਾਰ ਉਛਾਲਿਆ ਜਾਂਦਾ ਹੈ।ਨਾਲ ਹੀ, ਇਕ ਪਟ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਵੀ ਪਤਾ ਕਰੋ।
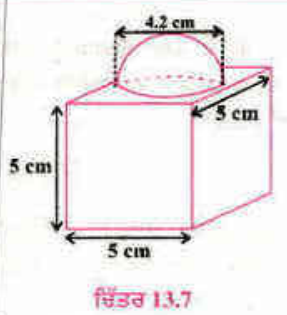
View Solutionਚਿੱਤਰ 13.7 ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਸਜਾਵਟ ਦੇ ਲਈ ਪ੍ਰਯੇਗ ਹੋਣ ਵਾਲਾ ਬਲਾਕ ਦੋ ਠੋਸਾਂ ਨਾਲ ਮਿਲ ਕੇ ਬਣਿਆ ਹੈ। ਇਨ੍ਹਾਂ ਵਿੱਚ ਇੱਕ ਘਣ ਹੈ ਅਤੇ ਦੂਸਰਾ ਅਰਧ ਗੋਲਾ ਹੈ। ਇਸ ਬਲਾਕ ਦਾ ਆਧਾਰ 5cm ਭੁਜਾ ਜਾਂ ਕਿਨਾਰੇ ਵਾਲਾ ਇੱਕ ਘਣ ਹੈ ਅਤੇ ਉਸਦੇ ਉੱਪਰ ਲੱਗੇ ਹੋਏ ਅਰਧ ਗ਼ੋਲੋ ਦਾ ਵਿਆਸ 4.2 cm ਹੈ। ਇਸ ਬਲਾਕ ਦੀ ਸੰਪੂਰਨ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋਂ (π=227 ਲਓ।)
View Solution5.5 ਮੀ. ਲੰਬੇ ਅਤੇ 4 ਮੀ. ਚੌੜੇ ਕਮਰੇ ਦੇ ਬਾਹਰਵਾਰ ਚਾਰੇ ਪਾਸੇ 2.25 ਮੀ. ਚੌੜਾ ਇੱਕ ਬਰਾਂਡਾ ਬਣਾਇਆ ਗਿਆ ਹੈ। ਪਤਾ ਕਰੋ (i) ਬਰਾਂਡੇ ਦਾ ਖੇਤਰਫਲ (ii) ₹200 ਪ੍ਰਤੀ 1 ਮੀ.^2 ਦੀ ਦਰ ਨਾਲ ਬਰਾਂਡੇ ਦੇ ਫਰਸ਼ 'ਤੇ ਸੀਮਿੰਟ ਕਰਵਾਉਣ ਦਾ ਖਰਚ।
View Solutionਸਿੱਧ ਕਰੋ ਕਿ A={1,2,3,4,5} ਵਿੱਚ R={(a,b):|a–b| ਜਿਸਤ ਹੈ।} ਰਾਹੀਂ ਦਿੱਤਾ ਸੰਬੰਧ R ਇੱਕ ਸਮਤੁਲ ਸੰਬੰਧ ਹੈ। ਪ੍ਰਮਾਣਿਤ ਕਰੋ ਕਿ {1, 3, 5} ਦੇ ਸਾਰੇ ਤੱਤ ਇੱਕ ਦੂਜੇ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ਅਤੇ ਸਮੂਹ {2, 4} ਦੇ ਸਾਰੇ ਤੱਤ ਇੱਕ ਦੂਜੇ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ਪਰੰਤੂ {1, 3, 5} ਦਾ ਕੋਈ ਵੀ ਤੱਤ {2, 4} ਦੇ ਕਿਸੇ ਤੱਤ ਨਾਲ ਸੰਬੰਧਿਤ ਨਹੀਂ ਹੈ।
View Solutionਮੰਨ ਲਓ ਕਿ XY- ਤਲ ਵਿੱਚ ਸਥਿਤ ਸਾਰੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਸਮੂਹ L ਹੈ ਅਤੇ L ਵਿੱਚ R={(L1,L2):L1 ਸਮਾਂਤਰ ਹੈ L2ਨਾਲ}ਰਾਹੀਂਪਰਿਭਾਸ਼ਿਤਸੰਬੰਧRਹੈ।ਸਿੱਧਕਰੋਕਿRਇੱਕਸਮਤੁੱਲਸੰਬੰਧਹੈ।ਰੇਖਾy = 2x + 4 ਨਾਲ ਸੰਬੰਧਿਤ ਸਾਰੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਸਮੂਹ ਪਤਾ ਕਰੋ।
View Solutionਸਿੱਧ ਕਰੋ ਕਿ ਹੇਠਾਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ f:N→N , ਇੱਕ-ਇੱਕ ਅਤੇ ਔਨਟੂ ਹੈ: f(x)={x+1ਜੇਕਰxਟਾਂਕਹੈx−1ਜੇਕਰxਜਿਸਤਹੈ
View Solutionਜੇਕਰ f(x)=3x+45x−7 ਰਾਹੀਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ f:R−{75}→R−{35} ਅਤੇ g(x)=7x+45x−3 ਰਾਹੀਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ g:R−{35}→R−{75} ਦਿੱਤਾ ਹੈ, ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ fog=IA ਅਤੇ gof=IB ਹਨ। ਇਸ ਤਰ੍ਹਾਂ ਕਿ IA(x)=x,∀x∈A ਅਤੇ IB(x)=x,∀x∈B, ਜਿੱਥੇ A = R -{3/5}, B = R - {7/5}ਹਨ।I_AਅਤੇI_B ਨੂੰ ਕ੍ਰਮਵਾਰ ਸਮੂਹਾਂ A ਅਤੇ B ਦੇ ਤਤਸਮਕ ਫਲਨ ਕਹਿੰਦੇ ਹਨ।
View SolutionSuppose A = {– 1, 0, 1, 2} , B = {– 4, – 2, 0, 2} And f, g : A rarr B , Respectively f (x) = x^2 – x , x in A And g (x) = 2 | x- (1/2) | -1, x in A ਰਾਹੀਂ ਪਰਿਭਾਸ਼ਿਤ ਫਲਨ ਹਨ, ਕੀ f ਅਤੇ g ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
View Solution(x+1)n ਦੇ ਪ੍ਰਸਾਰ ਵਿੱਚ (r−1)ਵੇਂ, rਵੇਂ ਅਤੇ (r+1)ਵੇਂ ਪਦਾਂ ਦੇ ਗੁਣਾਂਕਾਂ ਦਾ ਅਨੁਪਾਤ 1:3:5 ਹੈ, n ਅਤੇ r ਪਤਾ ਕਰੋ।
View Solutionਬਿੰਦੂਆਂ (1, -2, 3) ਅਤੇ (3, 4, -5) ਨੂੰ ਮਿਲਾਉਣ ਤੋਂ ਬਣੇ ਰੇਖਾ ਖੰਡ ਨੂੰ ਅਨੁਪਾਤ 2 : 3 ਵਿੱਚ (i) ਅੰਦਰੂਨੀ ਤੌਰ ਤੇ (ii) ਬਾਹਰੀ ਤੌਰ 'ਤੇ ਵੰਡਣ ਵਾਲੇ ਬਿੰਦੂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੇ।
View Solutionਇੱਕ ਸਿੱਕੇ ਨੂੰ ਤਿੰਨ ਵਾਰੀ ਉਛਾਲਿਆ ਗਿਆ ਹੈ। ਹੇਠ ਲਿਖੀਆਂ ਘਟਨਾਵਾਂ ਤੇ ਵਿਚਾਰ ਕਰੋ A: “ਕੋਈ ਚਿਤ ਪਰਗਟ ਨਹੀਂ ਹੁੰਦਾ ਹੈ, B: 'ਠੀਕ ਇੱਕ ਚਿਤ ਪ੍ਰਗਟ ਹੁੰਦਾ ਹੈ' ਅਤੇ C: 'ਘੱਟੋ-ਘੱਟ ਦੋ ਚਿਤ ਪ੍ਰਗਟ ਹੁੰਦੇ ਹਨ” । ਕੀ ਇਹ ਪਰਸਪਰ ਨਿਵੇਕਲੀ ਅਤੇ ਸਰਵਾਂਗੀ ਘਟਨਾਵਾਂ ਦਾ ਸਮੂਹ ਹੈ ?
View Solutionਨਿਮਨਲਿਖਤ ਅਸਮਾਨਤਾਵਾਂ ਪ੍ਰਣਾਲੀ : 2x+y≤10,x+3y≤15,x,y≥0 ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਉਪਯੁਕਤ ਖੇਤਰ ਦੇ ਕੋਨਾ ਬਿੰਦੂ : (0,0),(5,0),(3,4) ਅਤੇ (0,5) ਹਨ। ਮੰਨ ਲਉ ਕਿ Z=px+qy, ਜਿੱਥੇ p,q>0, p ਅਤੇ q ਦੇ ਲਈ ਨਿਮਨਲਿਖਤ ਵਿੱਚ ਕਿਹੜਾ ਪ੍ਰਤੀਬੰਧ ਉਚਿਤ ਹੈ ਤਾਂ ਕਿ Z ਦਾ ਅਧਿਕਤਮ ਮੁੱਲ, (3,4) ਅਤੇ (0,5) ਦੋਵਾਂ ਤੇ ਘਟਿਤ ਹੁੰਦਾ ਹੈ।
View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ P(A)=12,P(A∪B)=35 ਅਤੇ P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਆਪਸ ਵਿੱਚ ਨਿਵੇਕਲੀਆਂ ਹਨ
View SolutionA ਅਤੇ B ਇਹੋ ਜਿਹੀ ਘਟਨਾਵਾਂ ਦਿੱਤੀਆਂ ਹਨ ਜਿੱਥੇ P(A)=12,P(A∪B)=35 ਅਤੇ P(B) ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਜੇਕਰ ਘਟਨਾਵਾਂ ਅਜ਼ਾਦ ਹਨ।
View Solutionਦਿੱਤੀ ਹੋਈ ਘਟਨਾਵਾਂ A ਅਤੇ B ਇਹੋ ਜਿਹੀਆਂ ਹਨ, ਜਿੱਥੇ P(A)=14,P(B)=12 ਅਤੇ P(A∩B)=18 ਤਾਂ P(AਨਹੀਂਅਤੇBਨਹੀਂ) ਪਤਾ ਕਰੋ।
View SolutionA.P.:3/2,1/2,-1/2,-3/2........ ਦੇ ਲਈ ਪਹਿਲਾ ਪਦ a ਅਤੇ ਸਾਝਾ ਅੰਤਰ d ਲਿਖੋ।
View Solution
