ਗੁਣਨਖੰਡ ਥਿਊਰਮ ਲਾਗੂ ਕਰਕੇ ਦੱਸੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਥਿਤੀਆਂ ਵਿਚੋਂ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ g(x) , p(x) ਦਾ ਇਕ ਗੁਣਨਖੰਡ ਹੈ ਜਾਂ ਨਹੀਂ:-p(x)=x3+3x2+3x+1,g(x)=x+2
Step by step video & image solution for ਗੁਣਨਖੰਡ ਥਿਊਰਮ ਲਾਗੂ ਕਰਕੇ ਦੱਸੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਥਿਤੀਆਂ ਵਿਚੋਂ ਹਰੇਕ ਸਥਿਤੀ ਵਿੱਚ g(x) , p(x) ਦਾ ਇਕ ਗੁਣਨਖੰਡ ਹੈ ਜਾਂ ਨਹੀਂ:-p(x) = x^3 + 3x^2+ 3x + 1, g(x) = x + 2 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ਹੇਠ ਲਿਖੇ ਬਹੁਪਦ ਦੀ ਘਾਤ ਲਿਖੋ:- x5−x4+3
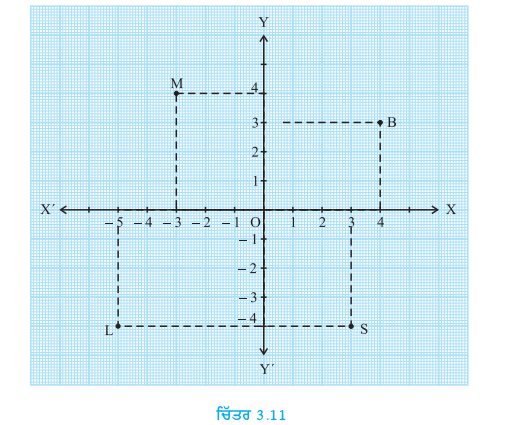
View Solutionਚਿੱਤਰ 3.11 ਦੇਖਕੇ ਹੇਠ ਲਿਖੇ ਕਥਨ ਨੂੰ ਪੂਰਾ ਕਰੋ:- ਬਿੰਦੂ B ਦਾ ਭੁਜ ਅਤੇ ਕੋਟੀ ਕੁਮਵਾਰ _ _ _ _ ਅਤੇ _ _ _ _ ਹਨ। ਇਸ ਲਈ B ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (___,__ ) ਹਨ।
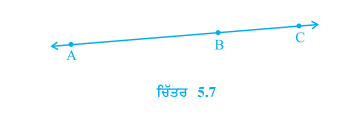
View Solutionਜੇ A,B ਅਤੇ C ਇਕ ਰੇਖਾ 'ਤੇ ਸਥਿਤ ਤਿੰਨ ਬਿੰਦੂ ਹਨ ਅਤੇ B ਬਿੰਦੂਆਂ A ਅਤੇ C ਦੇ ਵਿਚਾਲੇ ਸਥਿਤ ਹੈ(ਦੇਖੋ ਚਿੱਤਰ 5.7), ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ AB+BC=AC ਹੈ।
View Solutionp(x) को g(x) से भाग दीजिए , जबकि p(x)=x=3x2−1 और g(x)=1+x.
View Solutionज्ञात कीजिए कि क्या g(x),p(x) का एक गुणनखण्ड है । यदि p(x)=x3+x2+3x+175 तथा g(x)=(x+5)?
View Solutionगुणनखण्ड प्रमेय लागु करके बताइए कि स्थिति में g(x),p(x) का गुणनखण्ड है या नहीं :
p(x)=x3+3x2+3x+1,g(x)=x+2
View Solutionविभाजन एल्गोरिथ्म का प्रयोग करके, निम्न में p (x ) को g (x ) से भाग देने पर भागफल तथा शेषफल ज्ञात कीजिए :
p(x)=3x2−x3−3x+5,g(x)=x−1−x2
View SolutionDivide p(x)byq(x)p(x)=2x^(2)+3x+1,g(x)=x+2
View SolutionDetermine whether g (x) is a factor of P (x) using the factor theorem for each of the following: (i) P (x) = x^3 + 3x^2 + 3x + 1, g(x) = x + 2
View SolutionDivide p(x)by g(x), where p(x) = p(x)=x+3x2−1and g(x)=1+x
View SolutionDivide p(x) by g(x), where p(x)=x+3x2−1 and g(x)=1+x.
View SolutionUse the factor theorem to determine whether g(x) is a factor of p(x) in each of the following cases :
p(x)+x3+3x2+3x+1,g(x)=x+2
View SolutionCheck that p(x),g(x) Whether or not there is a multiple of p(x)=x^(3)-x+1 And g(x)=2-3x is.
View Solutionp(x) ਨੂੰ g(x) ਨਾਲ ਭਾਗ ਕਰੋ, ਜਿੱਥੇ p(x)=x+3x2–1 ਅਤੇ g(x) = 1 + x ਹੈ।
View SolutionUse the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases: p(x)=x3+3x2+3x+1,g(x)=x+2
View Solution
