ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ P 'ਤੇ ਕੱਟਦੇ ਹਨ। ਦਰਸਾਉ ਕਿ ar (APB) × ar (CPD) = ar (APD) × ar (BPC) ਹੈ। [ਸੰਕੇਤ: A ਅਤੇ C ਤੋਂ BD ਉੱਤੇ ਲੰਬ ਖਿੱਚੋ।
Step by step video & image solution for ਚਤੁਰਭੁਜ ABCD ਦੇ ਵਿਕਰਣ AC ਅਤੇ BD ਆਪਸ ਵਿਚ ਬਿੰਦੂ P 'ਤੇ ਕੱਟਦੇ ਹਨ। ਦਰਸਾਉ ਕਿ ar (APB) × ar (CPD) = ar (APD) × ar (BPC) ਹੈ। [ਸੰਕੇਤ: A ਅਤੇ C ਤੋਂ BD ਉੱਤੇ ਲੰਬ ਖਿੱਚੋ। by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
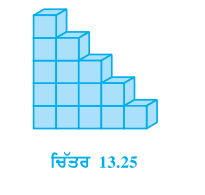
ਇਕ ਬੱਚਾ ਭਵਨ ਬਲਾਕਾਂ ਨਾਲ ਖੇਡ ਰਿਹਾ ਹੈ ਜਿਹੜੇ ਇਕ ਘਣ ਅਕਾਰ ਦੇ ਹਨ। ਉਸ ਨੇ ਚਿਤਰ 13.25 ਵਿੱਚ ਦਰਸਾਏ ਅਨੁਸਾਰ ਇਕ ਢਾਂਚਾ ਬਣਾਇਆ ਹੈ। ਹਰੇਕ ਘਣ ਦਾ ਕਿਨਾਰਾ 3 ਸਮ ਹੈ। ਉਸ ਬੱਚਾ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਢਾਂਚੇ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ
View Solutionਹੇਠ ਦਿੱਤੇ ਕਥਨ ਸਹੀ ਹਨ ਜਾਂ ਗਲਤ ?ਕਾਰਨ ਸਹਿਤ ਉੱਤਰ ਦਿਉ:-ਹਰੇਕ ਪੂਰਨ ਸੰਖਿਆ ਇੱਕ ਪ੍ਰਾਕ੍ਰਿਤਿਕ ਸੰਖਿਆ ਹੁੰਦੀ ਹੈ।
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
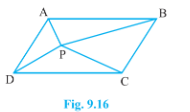
View Solutionआकृति में में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि
(i) ar(APB)+ar(PCD)=12ar(ABCD)
(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु P पर प्रतिच्छेद करते है दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है ।
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि
ar(APB)×ar(CPD)=ar(APD)×ar(BPC)
View Solutionदिए गए चित्र में P समांतर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है |दर्शाइए की
(i)ar(APB)+ar(PCD)=12ar(ABCD)
ar(APD)+ar(PBC)=ar(APB)+ar(PCD)

View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है। दर्शाइए कि ar(APB)×ar(CPD)=ar(APD)×ar(BPC) है।
संकेत : A और C से BD पर लम्ब खींचिए
View Solutionचतुर्भुज ABCD के विकर्ण AC और BD परस्पर चतुर्भुज के भीतर काटते है तो
ar(ABCD)=ar(ABC)+ar(…….).
View SolutionIn P is a point in the interior of a parallelogram ABCD. Show that<br>(ii)ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
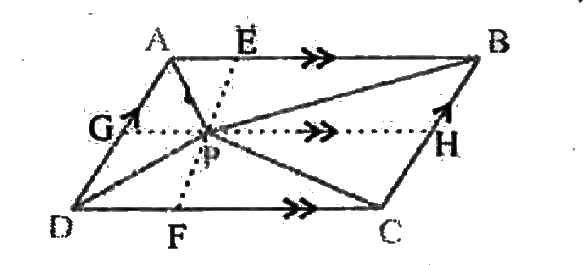
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPD).
[Hint : From A and C, draw perpendiculars to BD.
View SolutionIN the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = 12 ar (ABCD)
(ii) ar (APD) + ar(PBC) = ar(APB) + ar (PCD)
View SolutionDiagonals AC and BD of a quadrilateral ABCD each other at P. Show that ar (APB) × ar (CPD) =ar (APD) × ar (BPC)
View SolutionIn the given figure, P is any point located in the interior of the parallelogram ABCD. Indicate that (i) ar (Delta APB ) + ar (Delta PCD ) = (1)/(2) (ar||^(g m)ABCD) (Ii) ar(Delta APD) + ar(Delta BPC ) = ar(Delta APB) + ar(Delta PCD)
View SolutionDiagonals AC and BD of quadrilateral ABCD intersect each other at P. Show that ar (APB)×ar(CPD) = ar (APD)×ar(BPC).
View Solution