A straight glass tube has two inlets X and Y at the two ends. The length of the tube is 200 cm. HCl gas through inlet X and NH3 gas through inlet Y are allowed to enter the tube at the same time. White fumes first appear at a point Pinside the tube. Find the distance of P from X.
To solve the problem, we will use Graham's Law of Effusion which states that the rate of effusion of a gas is inversely proportional to the square root of its molar mass.
1. Identify the gases and their molar masses:
- HCl (Hydrochloric acid) has a molar mass of approximately 36.5 g/mol.
- NH3 (Ammonia) has a molar mass of approximately 17 g/mol.
2. Set up the problem:
- Let the distance from inlet X (where HCl is introduced) to point P be x cm.
- Therefore, the distance from inlet Y (where NH3 is introduced) to point P will be 200−x cm, since the total length of the tube is 200 cm.
3. Apply Graham's Law:
- According to Graham's Law, the ratio of the distances traveled by the two gases is inversely proportional to the square root of their molar masses:
200−xx=√MHCl√MNH3
Where MHCl=36.5 g/mol and MNH3=17 g/mol.
4. Substitute the molar masses into the equation:
200−xx=√36.5√17
5. Calculate the square roots:
- √36.5≈6.04
- √17≈4.12
6. Set up the equation:
200−xx=6.044.12
7. Cross-multiply to solve for x:
4.12(200−x)=6.04x
8. Expand and rearrange the equation:
824−4.12x=6.04x
824=6.04x+4.12x
824=10.16x
9. Solve for x:
x=82410.16≈81.22 cm
10. Conclusion:
The distance of point P from inlet X is approximately 81.22 cm.
- HCl (Hydrochloric acid) has a molar mass of approximately 36.5 g/mol.
- NH3 (Ammonia) has a molar mass of approximately 17 g/mol.
- Let the distance from inlet X (where HCl is introduced) to point P be x cm.
- Therefore, the distance from inlet Y (where NH3 is introduced) to point P will be 200−x cm, since the total length of the tube is 200 cm.
- According to Graham's Law, the ratio of the distances traveled by the two gases is inversely proportional to the square root of their molar masses:
200−xx=√MHCl√MNH3
Where MHCl=36.5 g/mol and MNH3=17 g/mol.
200−xx=√36.5√17
- √36.5≈6.04
- √17≈4.12
200−xx=6.044.12
4.12(200−x)=6.04x
824−4.12x=6.04x
824=6.04x+4.12x
824=10.16x
x=82410.16≈81.22 cm
The distance of point P from inlet X is approximately 81.22 cm.
Topper's Solved these Questions
- STATES OF MATTER : GASES AND LIQUIDSBOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - REVIEW EXERCISES
45 Videos
- STATES OF MATTER : GASES AND LIQUIDSBOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
20 Videos
- SOME P-BLOCK ELEMENTS BOOK - ICSECHAPTER - SOME P-BLOCK ELEMENTS EXERCISE - NCERT TEXTBOOK EXERCISES (With Hints and Solutions)
63 Videos
- STRUCTURE OF ATOMBOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - NCERT Textbook Exercises
67 Videos
Similar Questions
A straight glass tube has two inlets X and Y at the two ends. The length of the tube is 100 cm. HCl gas through inlet X and NH3 gas through inlet Y are allowed to enter the tube at the same time. White fumes appear at a point P inside the tube. Find the distance of P from X.
View SolutionThrough the two ends of a glass tube of length 200cm hydrogen chloride gas and ammonia are allowed to enter At what distance ammonium chloride will first appear ? .
View SolutionA line through point A(1,3) and parallel to the line x-y+1 = 0 meets the line 2x-3y + 9 = 0 at point P. Find distance AP without finding point P.
View SolutionA line is drawn through the point A(4,−1) and parallel to the line 3x−4y+7=0. Find the coordinates of two points on this line which are at distance of 5 units from A.
View SolutionA steel tube of length 1.00 m is struck at one end. A person with his ear close to the other end hears the sound of the blow twice one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings.
View Solutiona line drawn through A(4,−1) parallel to the line 3x−4y+1=0. Find the coordinates of two points on this line which are at a distance of 5 units from A
View SolutionFind the equation of a curve passing through the point (1.1) if the perpendicular distance of the origin from the normal at any point P(x, y) of the curve is equal to the distance of P from the x-axis.
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then
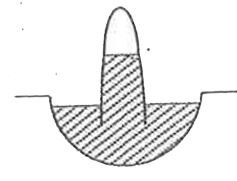
A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View SolutionIn an organ pipe ( may be closed or open of 99cm length standing wave is setup , whose equation is given by longitudinal displacement ξ=(0.1mm)cos(2π)0.8(y+1cm)cos2π(400)t
where y is measured from the top of the tube in metres and t in second. Here 1cm is th end correction.

Assume end correction approximately equals to (0.3)×(diameter of tube) , estimate the moles of air pressure inside the tube (Assume tube is at NTP , and at NTP,22.4litre contain 1mo≤)
View SolutionIn an organ pipe ( may be closed or open of 99cm length standing wave is setup , whose equation is given by longitudinal displacement ξ=(0.1mm)cos(2π)0.8(y+1cm)cos2π(400)t
where y is measured from the top of the tube in metres and t in second. Here 1cm is th end correction.

Assume end correction approximately equals to (0.3)×(diameter of tube) , estimate the moles of air pressure inside the tube (Assume tube is at NTP , and at NTP,22.4litre contain 1 mole)
View Solution