A seconds' pendulum is taken to a place where acceleration due to gravity falls to one-fourth. How is the time period of the pendulum affected, if at all ? Give reason. What will be its new time period ?
To solve the problem, we need to analyze how the time period of a seconds pendulum changes when the acceleration due to gravity is reduced to one-fourth of its original value.
1. Understanding the Time Period Formula:
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
2. Identifying the Initial Conditions:
A seconds pendulum has a time period of 2 seconds. This means that at the original location, the time period T is:
T=2 seconds
Therefore, we can express it as:
2=2π√Lg
3. New Acceleration Due to Gravity:
If the acceleration due to gravity falls to one-fourth, we can denote the new gravity as:
g′=g4
4. Calculating the New Time Period:
We need to find the new time period T′ at the new location. Substituting g′ into the time period formula:
T′=2π√Lg′
Replacing g′ with g4:
T′=2π
⎷Lg4=2π√4Lg=2π⋅2√Lg=4π√Lg
Since 2π√Lg=2 seconds (the original time period), we have:
T′=4 seconds
5. Conclusion:
The new time period of the pendulum when taken to a place where the acceleration due to gravity is one-fourth is:
T′=4 seconds
Summary:
- The time period of the pendulum increases when the acceleration due to gravity decreases.
- The new time period is 4 seconds.
The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where:
- T is the time period,
- L is the length of the pendulum,
- g is the acceleration due to gravity.
A seconds pendulum has a time period of 2 seconds. This means that at the original location, the time period T is:
T=2 seconds
Therefore, we can express it as:
2=2π√Lg
If the acceleration due to gravity falls to one-fourth, we can denote the new gravity as:
g′=g4
We need to find the new time period T′ at the new location. Substituting g′ into the time period formula:
T′=2π√Lg′
Replacing g′ with g4:
T′=2π
⎷Lg4=2π√4Lg=2π⋅2√Lg=4π√Lg
Since 2π√Lg=2 seconds (the original time period), we have:
T′=4 seconds
The new time period of the pendulum when taken to a place where the acceleration due to gravity is one-fourth is:
T′=4 seconds
- The time period of the pendulum increases when the acceleration due to gravity decreases.
- The new time period is 4 seconds.
Topper's Solved these Questions
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 1 INTERNATIONAL SYSTEM OF UNITS (2 Marks Questions )
Explore 9 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:TOPIC 1 INTERNATIONAL SYSTEM OF UNITS (3 Marks Questions )
Explore 16 Videos
- MEASUREMENTS AND EXPERIMENTATION Book:ICSEChapter:MEASUREMENTS AND EXPERIMENTATION Exercise:EXERCISE 1(C) (Mulitple Choice Type)
Explore 3 Videos
- MAGNETISM Book:ICSEChapter:MAGNETISM Exercise:EXERCISE-10(B) (Multiple Choice Type)
Explore 2 Videos
- MOTION IN ONE DIMENSION Book:ICSEChapter:MOTION IN ONE DIMENSION Exercise:EXERCISE -2 (C) ( Multiple choice type :)
Explore 17 Videos
Similar Questions
The time period of a seconds' pendulum :
View SolutionIf a Seconds pendulum is moved to a planet where acceleration due to gravity is 4 times, the length of the second's pendulum on the planet should be made
View SolutionHow is the time period of a simple pendulum affected, if at all, in the following situation
the length is made four times.
View SolutionA second pendulum is moved to moon where acceleration dur to gravity is 1/6 times that of the earth, the length of the second pendulum on moon would be
View Solution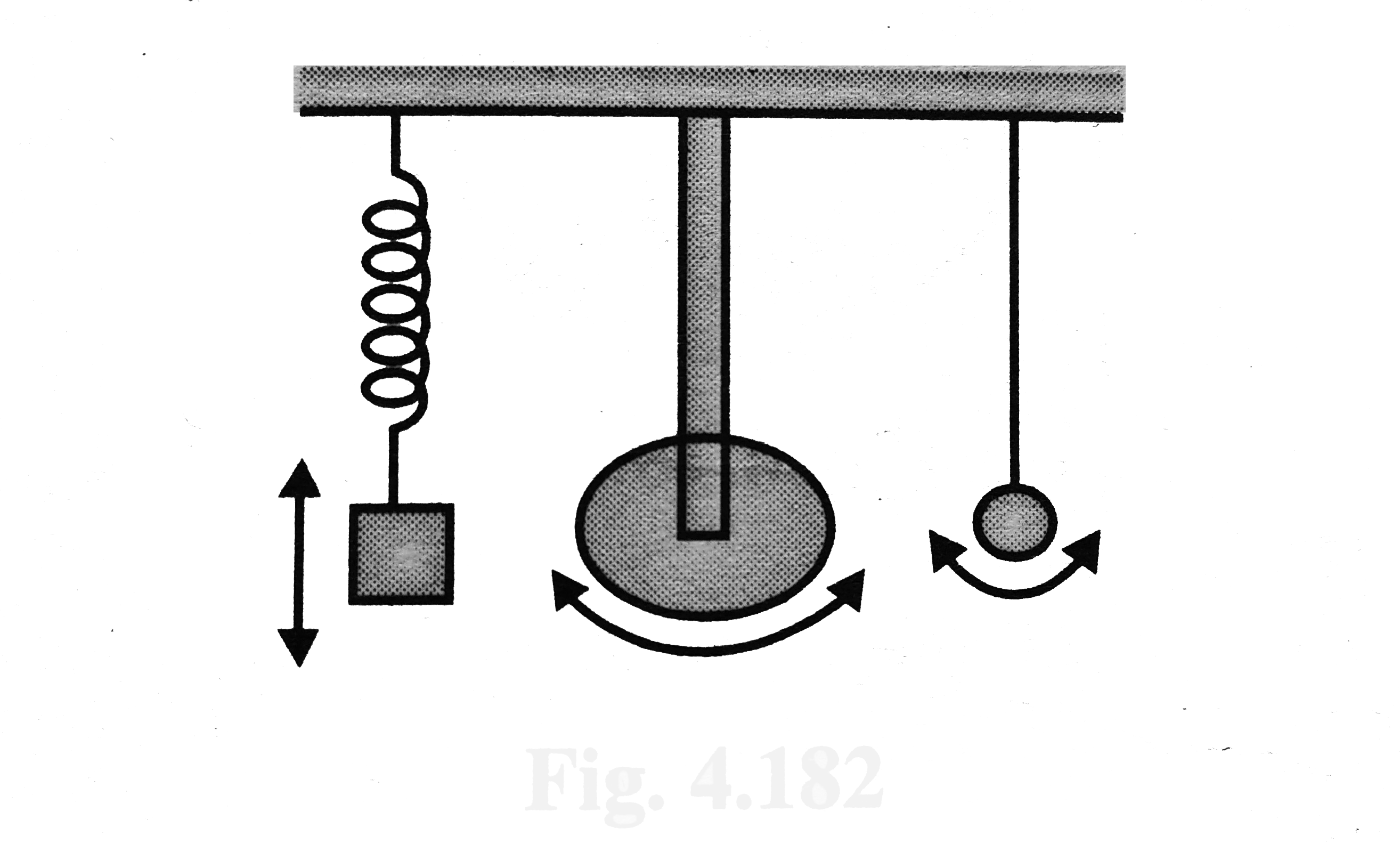
Q. Statement I Three pendulums are suspended from ceiling as shown in Fig. These three pendulums are set to oscillate as shon by arrows, and it is found that all three have same time period. Noe, all three are taken to a place where acceleration due to gravity changes to 4/9th of its value at the first place. If spring pendulum makes 60 cycles in a given time at this place, then torsion pendulum and simple pendulum will also make 60 oscillation in same (given) time interval. Statement II: Time period of torsion pendulum is independent of acceleration due to gravity.
View SolutionHow would the time period of a simple pendulum be affected if (a) the length is doubled (b) the amplitude is doubled ?
View SolutionState how does the time period of a simple pendulum depend on mass of bob.
View SolutionA cabin is falling freely under gravity, what is the time period of a pendulum attached to its celling?
View SolutionTime period of a simple pendulum in a freely falling lift will be
View SolutionIf a simple pendulum is taken to place where g decreases by 2%, then the time period
View Solution