In a hexagon, ABCDEF, side AB is parallel to side FE and ∠B:∠C:∠D:∠E=6:4:2:3 Find ∠Band∠D.
The correct Answer is:∠B=216∘,∠C=144∘,∠D=72∘and∠E=108∘
To solve the problem, we need to find the values of angle B and angle D in the hexagon ABCDEF, given that side AB is parallel to side FE and the angles B, C, D, and E are in the ratio 6:4:2:3.
1. Understanding the Properties of the Hexagon:
Since AB is parallel to FE, we know that the sum of angles A and F will be 180 degrees. This is due to the property of alternate interior angles formed by a transversal line cutting through parallel lines.
Hint: Remember that when two lines are parallel, the angles on the same side of the transversal add up to 180 degrees.
2. Sum of Interior Angles of a Hexagon:
The formula to calculate the sum of the interior angles of a polygon is (n - 2) × 180 degrees, where n is the number of sides. For a hexagon (n = 6):
Sum of interior angles=(6−2)×180=720 degrees
Hint: Use the formula for the sum of interior angles to find the total angle measure for any polygon.
3. Setting Up the Angles:
Let the angles B, C, D, and E be represented in terms of a variable x based on their given ratio:
- Angle B = 6x
- Angle C = 4x
- Angle D = 2x
- Angle E = 3x
Hint: When dealing with ratios, express each part of the ratio in terms of a common variable.
4. Expressing the Total Angle Sum:
The total sum of the angles in the hexagon can be expressed as:
Angle A+Angle B+Angle C+Angle D+Angle E+Angle F=720 degrees
Since angle A + angle F = 180 degrees (from step 1), we can substitute:
180+(6x+4x+2x+3x)=720
Hint: Substitute known values to simplify the equation.
5. Simplifying the Equation:
Combine the angles:
180+15x=720
Now, isolate x:
15x=720−180
15x=540
x=54015=36 degrees
Hint: Isolate the variable by performing inverse operations.
6. Finding Angle B and Angle D:
Now that we have x, we can find the angles:
- Angle B = 6x = 6 × 36 = 216 degrees
- Angle D = 2x = 2 × 36 = 72 degrees
Hint: Substitute the value of x back into the expressions for angles to find their measures.
Final Answer:
- Angle B = 216 degrees
- Angle D = 72 degrees
Since AB is parallel to FE, we know that the sum of angles A and F will be 180 degrees. This is due to the property of alternate interior angles formed by a transversal line cutting through parallel lines.
The formula to calculate the sum of the interior angles of a polygon is (n - 2) × 180 degrees, where n is the number of sides. For a hexagon (n = 6):
Sum of interior angles=(6−2)×180=720 degrees
Let the angles B, C, D, and E be represented in terms of a variable x based on their given ratio:
- Angle B = 6x
- Angle C = 4x
- Angle D = 2x
- Angle E = 3x
The total sum of the angles in the hexagon can be expressed as:
Angle A+Angle B+Angle C+Angle D+Angle E+Angle F=720 degrees
Since angle A + angle F = 180 degrees (from step 1), we can substitute:
180+(6x+4x+2x+3x)=720
Combine the angles:
180+15x=720
Now, isolate x:
15x=720−180
15x=540
x=54015=36 degrees
Now that we have x, we can find the angles:
- Angle B = 6x = 6 × 36 = 216 degrees
- Angle D = 2x = 2 × 36 = 72 degrees
- Angle B = 216 degrees
- Angle D = 72 degrees
Topper's Solved these Questions
- UNDERSTANDING SHAPESBOOK - ICSECHAPTER - UNDERSTANDING SHAPESEXERCISE - Exercise 16B
20 Videos
- UNDERSTANDING SHAPESBOOK - ICSECHAPTER - UNDERSTANDING SHAPESEXERCISE - Exercise 16C
15 Videos
- UNDERSTANDING SHAPESBOOK - ICSECHAPTER - UNDERSTANDING SHAPESEXERCISE - Exercise 16C
15 Videos
- SURFACE AREA, VOLUME AND CAPACITY. BOOK - ICSECHAPTER - SURFACE AREA, VOLUME AND CAPACITY. EXERCISE - EXERCISE ( E )
11 Videos
Similar Questions
In a pentagon ABCDE, AB is parallel to DC and ∠A:∠E:∠D=3:4:5. Find angle E.
View SolutionIn a pentagon ABCDE, AB is parallel to DC and ∠A:∠E:∠D=3:4:5. Find angle E.
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC. If ∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrialateral ABCD.
View SolutionFind ∠A+∠B+∠C+∠D
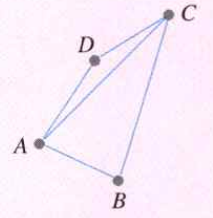
View SolutionIn a pentagon ABCDE, AB is parallel to ED and angle B=140∘. Find the angles C and D, if ∠C:∠D=5:6
View SolutionThe figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B:∠C:∠D=5:6:7.
(i) Using formula, find the sum of interior angles of the pentagon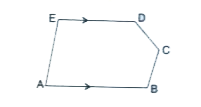
(ii) Write the value of ∠A+∠E.
(iii) Find angles B,C and D
View SolutionIn the given figure, find ∠D and ∠B.

View SolutionIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D of R and of ∠Dand∠A at S, then PQRS is a (A) Rectangle (B) Rhombus (C) Parallelogram (D) Quadrilateral whose opposite angles are supplementary
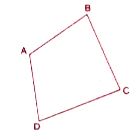
View SolutionIn quadrilateral ABCD, AB is the shortest side and DC is the longest side. Prove that :
(i) ∠B>∠D
(ii) ∠A>∠C
View SolutionA triangle ABC is such that 3∠A=4∠B=6∠C. Find the three angles.
View Solution