A rectangular field is 30 m in length and 22 m in width. Two mutually perpendicular roads, each 2.5 m wide, are drawn inside the field so that one road is parallel to the length of the field and the other road is parallel to its width. Calculate the area of the crossroads.
The correct Answer is:123.75m2
To solve the problem of finding the area of the crossroads formed by two mutually perpendicular roads inside a rectangular field, we will follow these steps:
Step 1: Understand the dimensions of the field and roads
The dimensions of the rectangular field are:
- Length = 30 m
- Width = 22 m
The width of each road is:
- Width of road = 2.5 m
Step 2: Calculate the area of the first road (R1)
The first road (R1) is parallel to the length of the field. The area of R1 can be calculated using the formula for the area of a rectangle:
Area of R1=Length×Width of road
Substituting the values:
Area of R1=30m×2.5m=75m2
Step 3: Calculate the area of the second road (R2)
The second road (R2) is parallel to the width of the field. The area of R2 is calculated similarly:
Area of R2=Width×Width of road
Substituting the values:
Area of R2=22m×2.5m=55m2
Step 4: Calculate the area of the overlapping square
The two roads overlap in the area of a square where they intersect. The area of this square can be calculated as:
Area of square=Width of road×Width of road
Substituting the values:
Area of square=2.5m×2.5m=6.25m2
Step 5: Calculate the total area of the crossroads
To find the total area of the crossroads, we add the areas of the two roads and subtract the area of the overlapping square:
Area of crossroads=Area of R1+Area of R2−Area of square
Substituting the calculated values:
Area of crossroads=75m2+55m2−6.25m2
Area of crossroads=130m2−6.25m2=123.75m2
Final Answer
The area of the crossroads is:
Area of crossroads=123.75m2
---
The dimensions of the rectangular field are:
- Length = 30 m
- Width = 22 m
- Width of road = 2.5 m
The first road (R1) is parallel to the length of the field. The area of R1 can be calculated using the formula for the area of a rectangle:
Area of R1=Length×Width of road
Substituting the values:
Area of R1=30m×2.5m=75m2
The second road (R2) is parallel to the width of the field. The area of R2 is calculated similarly:
Area of R2=Width×Width of road
Substituting the values:
Area of R2=22m×2.5m=55m2
The two roads overlap in the area of a square where they intersect. The area of this square can be calculated as:
Area of square=Width of road×Width of road
Substituting the values:
Area of square=2.5m×2.5m=6.25m2
To find the total area of the crossroads, we add the areas of the two roads and subtract the area of the overlapping square:
Area of crossroads=Area of R1+Area of R2−Area of square
Substituting the calculated values:
Area of crossroads=75m2+55m2−6.25m2
Area of crossroads=130m2−6.25m2=123.75m2
The area of the crossroads is:
Area of crossroads=123.75m2
Topper's Solved these Questions
- BOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(C )14videos
AREA OF A TRAPEZIUM AND A POLYGON
- BOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(D)21videos
AREA OF A TRAPEZIUM AND A POLYGON
- BOOK - ICSECHAPTER - AREA OF A TRAPEZIUM AND A POLYGONEXERCISE - EXERCISE 20(A)16videos
AREA OF A TRAPEZIUM AND A POLYGON
- BOOK - ICSECHAPTER - ALGEBRAIC EXPRESSIONS EXERCISE - Exercise 11(E)15videos
ALGEBRAIC EXPRESSIONS
- BOOK - ICSECHAPTER - CONSTRUCTION (USING RULER AND COMPASSES ONLY)EXERCISE - EXERCISE 18(D)10videos
CONSTRUCTION (USING RULER AND COMPASSES ONLY)
Similar Questions
There is a rectangular field of size 94 m×32 m. Three roads each of 2 m width pass through the field such that two roads are parallel to the breadth of the field and the third is parallel to the length. Calculate: (a) Area of the field covered by the three roads (b) Area of the field not covered by the roads.
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View Solution
Knowledge Check
- Question 1 - Select One
The perimeter of a rectangular field is 92m. If its length is 26m , find its breadth and area.
A20m;520m2B10m;510m2C20m;420m2D25m;580m2
A rectangular field is of length 60 m and breadth 35 m. Find the area of the field.
View SolutionA rectangular field is 154m long and 121m broad. A well of 14m length and 11m breadth is dug inside the field and mud taken out is spread evenly over the remaining part of the field to a thickness of 25cm. Find the depth of the well.
View SolutionA rectangular field has perimeter 186 m and breadth 35 m . Find its length .
View SolutionA rectangular grassy plot measures 90 m by 65 m. Two pathways, each 1.5m wide are running through the middle of the plot, parallel to its length and breadth. Find the area of the grassy portion.
View SolutionThrough a rectangular field of length 90 m and breadth 60 m, two roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the fields. If the width of each road is 3 m, find (i) the area covered by the roads. (ii) the cost of constructing the roads at the rate of Rs 110 per m2.
View SolutionA rectangular field is such that its length is one and a half times its breadth. A thick white line is drawn all along the edges of the field. If the total length of the white line is 200 m, find the length of the sides of the field.
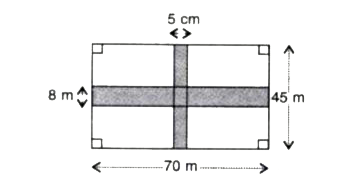
View SolutionThe adjoining figure shows a rectangular field 70m long and 45 m wide. The shaded portion shows two mutually perpendicular roads, one of width 5 m and the other with width 8 m. Find the cost of levelling the roads at the rate of Rs. 180 per sq. m.
 View Solution
View Solution

