Name a single transformation that maps P' to P''.
The correct Answer is:reflection in origin
To determine the single transformation that maps point P' to point P'', we can follow these steps:
1. Identify the Coordinates of Points:
- Let P' have coordinates (2, 2).
- Let P'' have coordinates (-2, -2).
2. Understand the Transformation:
- We need to find a transformation that takes the coordinates of P' and transforms them into the coordinates of P''.
3. Analyze the Change in Coordinates:
- The x-coordinate changes from 2 to -2, which indicates a reflection across the y-axis.
- The y-coordinate changes from 2 to -2, which indicates a reflection across the x-axis.
- However, if we consider both changes together, we can see that the transformation is actually a reflection through the origin.
4. Conclusion:
- The transformation that maps P' to P'' is a reflection through the origin.
5. Final Statement:
- Therefore, the single transformation that maps P' to P'' is the reflection in the origin.
- Let P' have coordinates (2, 2).
- Let P'' have coordinates (-2, -2).
- We need to find a transformation that takes the coordinates of P' and transforms them into the coordinates of P''.
- The x-coordinate changes from 2 to -2, which indicates a reflection across the y-axis.
- The y-coordinate changes from 2 to -2, which indicates a reflection across the x-axis.
- However, if we consider both changes together, we can see that the transformation is actually a reflection through the origin.
- The transformation that maps P' to P'' is a reflection through the origin.
- Therefore, the single transformation that maps P' to P'' is the reflection in the origin.
Similar Questions
Points (3, 0) and (-1,0) are invariant points under reflection in the line L1 points (0, -3) and (0, 1) are invariant points on reflection in line L2
State or describe a single transformation that maps P' onto P".
View SolutionPoint (-5,0) and (4,0) are invariant point under reflection in the line L1, point (0,-6) and (0,5) are invariant on reflection in the line L2 .
State or describe a single transformation that maps Q' onto Q'' .
View SolutionAttempt this question on graph paper.
Write down :
the single transformation that maps A' to A''.
View SolutionThe point A(-3, 2) is reflected in the x-axis to the point A'. Point A' is then reflected in the origin to point A".
Write down a single transformation that maps A onto A".
View SolutionThe point A(4, 6) is first reflected in the origin to point A'. Point A' is then reflected in the y-axis to point A".
Write down a single transformation that maps A onto A"
View SolutionThe triangle ABC, where A is (2, 6), B is (-3, 5) and C is (4, 7), is reflected in the y-axis to triangle A'B'C'. Triangle A'B'C' is then reflected in the origin to triangle A"B"C''.
Write down a single transformation that maps triangle ABC onto triangle A"B"C".
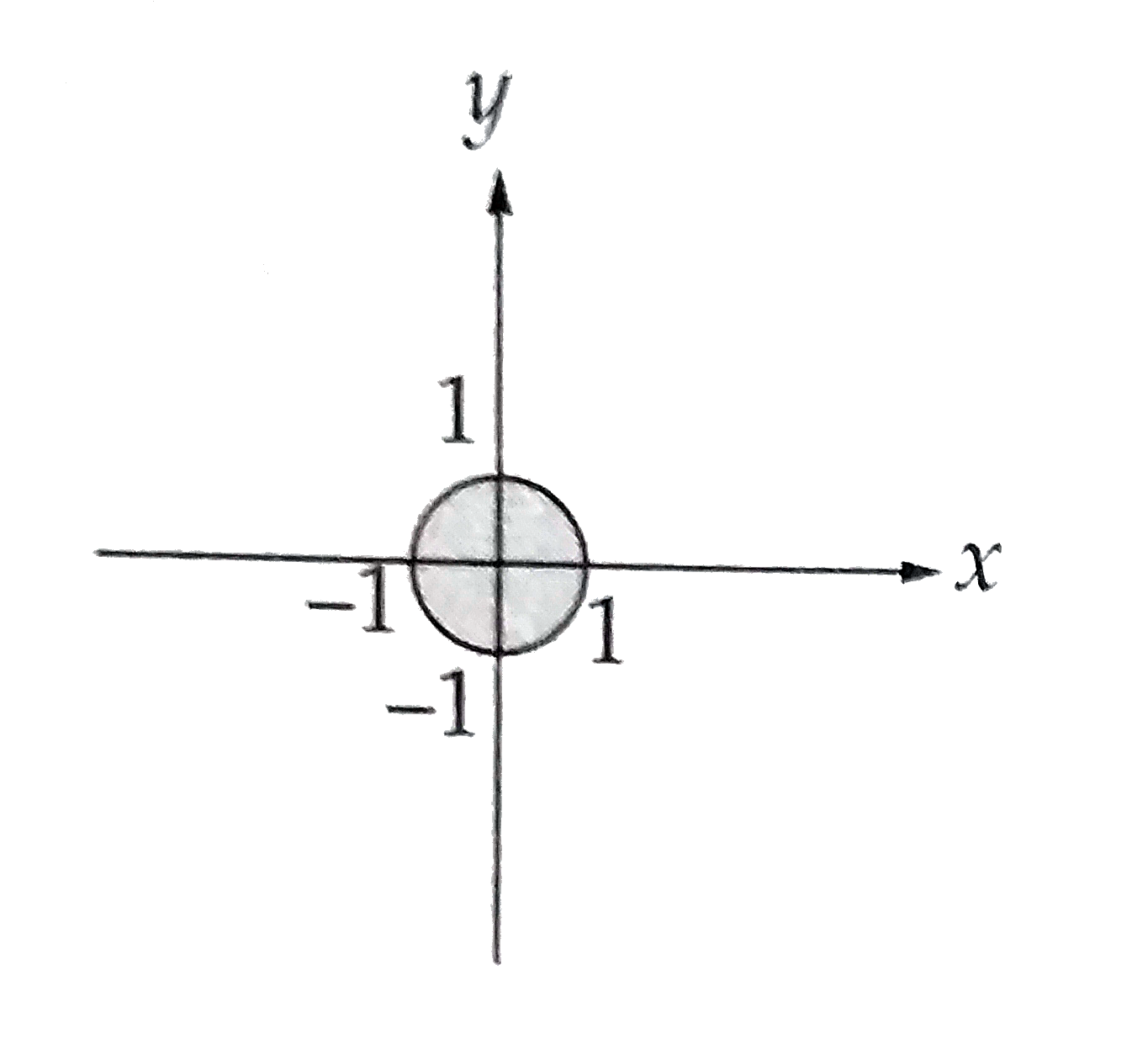
View SolutionThe shaed region represents the set C of all points (x, y) such that x2+y2≤1. The transformation T maps the point (x, y) to the point (2x, 4y). Which of the following shows the mapping of the set C by the transformation T ?
View SolutionWhich one of the following nuclear transformation is (n,p) type ?
View SolutionHow will you bring about the following transformations?
p-Methylacetophenone to benzene-1, 4-dicarboxylic acid (terephthalic acid)
View SolutionHow will you bring about the following transformations?
p-Methylacetophenone to benzene-1, 4-dicarboxylic acid (terephthalic acid)
View Solution
