The given figures shows a circle with centre O. Also , PQ = QR = RS and ∠PTS=75∘ Calculate:
(i) agn≤POS
(ii) ∠QOR
(iii) ∠PQR
(##SEL_RKB_ICSE_MAT_X_C17_E03_004_Q01.png" width="80%">
The correct Answer is:150∘(ii)50∘(iii)130∘
To solve the problem step by step, we will calculate the angles as requested.
Step 1: Understand the Given Information
We have a circle with center O. The chords PQ, QR, and RS are equal, and we are given that the angle PTS = 75 degrees.
Step 2: Calculate Angle POS
Using the property of circles, we know that the angle at the center (angle POS) is twice the angle at the circumference (angle PTS).
Angle POS=2×Angle PTS=2×75∘=150∘
Step 3: Calculate Angle QOR
Since PQ = QR = RS, the angles subtended by these chords at the center (angle POQ, angle QOR, and angle ROS) are equal. Let each of these angles be denoted as X.
From the previous step, we know that:
Angle POS=Angle POQ+Angle QOR+Angle ROS=150∘
Since all three angles are equal:
X+X+X=150∘⟹3X=150∘⟹X=50∘
Thus,
Angle QOR=50∘
Step 4: Calculate Angle PQR
In triangle OPQ, since OP = OQ (both are radii of the circle), we have an isosceles triangle. Therefore, the angles at P and Q are equal. Let these angles be denoted as Y.
Using the triangle sum property:
Angle OPQ+Angle OQP+Angle POQ=180∘
Substituting the known values:
Y+Y+50∘=180∘⟹2Y=130∘⟹Y=65∘
Thus,
Angle PQR=65∘
Summary of Results
(i) Angle POS = 150 degrees
(ii) Angle QOR = 50 degrees
(iii) Angle PQR = 65 degrees
We have a circle with center O. The chords PQ, QR, and RS are equal, and we are given that the angle PTS = 75 degrees.
Using the property of circles, we know that the angle at the center (angle POS) is twice the angle at the circumference (angle PTS).
Since PQ = QR = RS, the angles subtended by these chords at the center (angle POQ, angle QOR, and angle ROS) are equal. Let each of these angles be denoted as X.
Angle POS=Angle POQ+Angle QOR+Angle ROS=150∘
Since all three angles are equal:
X+X+X=150∘⟹3X=150∘⟹X=50∘
Thus,
Angle QOR=50∘
In triangle OPQ, since OP = OQ (both are radii of the circle), we have an isosceles triangle. Therefore, the angles at P and Q are equal. Let these angles be denoted as Y.
Angle OPQ+Angle OQP+Angle POQ=180∘
Substituting the known values:
Y+Y+50∘=180∘⟹2Y=130∘⟹Y=65∘
Thus,
Angle PQR=65∘
(i) Angle POS = 150 degrees
(ii) Angle QOR = 50 degrees
(iii) Angle PQR = 65 degrees
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(A)58videos
CIRCLES
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)16videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE39videos
CONSTRUCTIONS (CIRCLES)
Similar Questions
In the followoing figure , AD is the diameter of the circle with centre O. Chords AB,BC and CD are equal .If ∠DEF=110∘, Calculate :
(i) ∠AEF.
(ii) ∠FAB
(##SEL_RKB_ICSE_MAT_X_C17_E03_002_Q01.png" width="80%">View SolutionCalculate the angles x,y and z if
x3=y4=z5
(##SEL_RKB_ICSE_MAT_X_C17_E02_042_Q01.png" width="80%">View SolutionIn the given figure ,I is the incentre of triangle ABC . AI produced meets the circumcircle of the triangle ABC at point D. if ∠BAC=50∘and∠ABC=70∘, find :
(i) ∠BCD(ii)∠ICD(iii)∠BIC
(##SEL_RKB_ICSE_MAT_X_C17_E01_015_Q01.png" width="80%">View SolutionThe given figure shows a circle with centre O such that chord RS is parallel to chord QT, angle PRT=20∘ and angle POQ=100∘ calculate
(i) angle QTR
(ii) angle QRP
(iii) angle QRS
(iv) angle STR
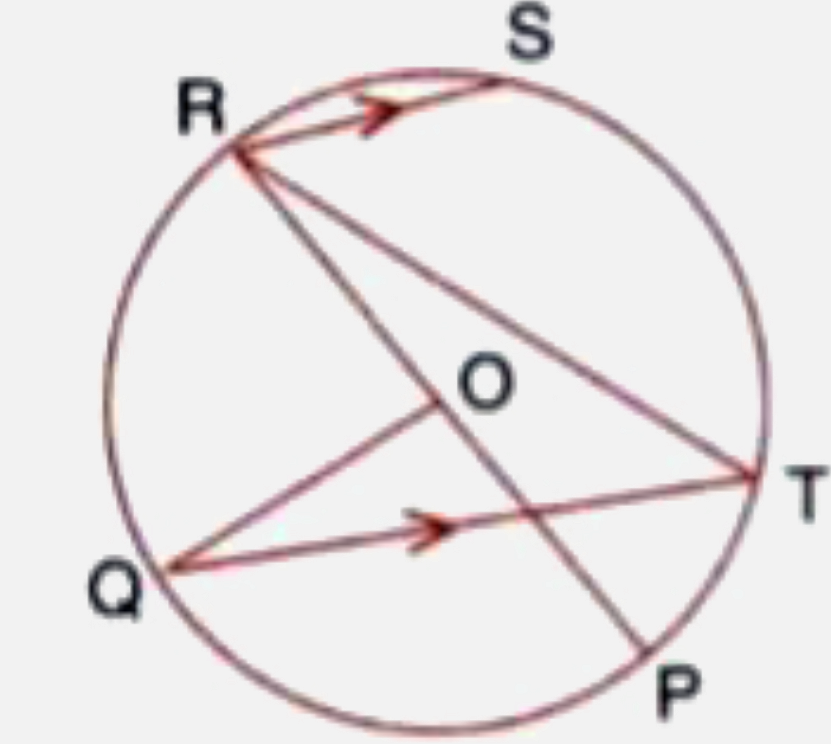 View Solution
View SolutionIn the following figure , angle B=90∘∠ADB=30∘and∠ACB=60∘
If ∠CD=m find AB .
(##SEL_RKB_ICSE_MAT_IX_CR_02_E01_162_Q01.png" width="80%">View SolutionIn the given figure ∠BAD=60∘,∠ABD=70∘∠BDC=45∘
(i) prove that AC is a diameter of the circle
(ii) Find ∠ACB
(##SEL_RKB_ICSE_MAT_X_C17_E02_002_Q01.png" width="80%">View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED
 View Solution
View SolutionIn the given figure. A is the centre of the circle , ABCD is a parallelogram and CDE is a straight line.
Prove that :∠BCD=2∠ABE
(##SEL_RKB_ICSE_MAT_X_C17_E02_036_Q01.png" width="80%">View SolutionTwo unequal circles with centres A and B intersect each other at points C and D. The centre B of the smaller circles lies on the circumference of the bigger circle with centre A. If ∠CMD=x∘, find in terms of x, the measure of angle DAC .
(##SEL_RKB_ICSE_MAT_X_C17_E01_013_Q01.png" width="80%">View SolutionThe given figure shows a semi circle with centre O ane diameter PQ. If PA=AB and ∠BCQ=140∘ find measures of angles PAB and AQB. Also, show that AO is parallel to BQ.
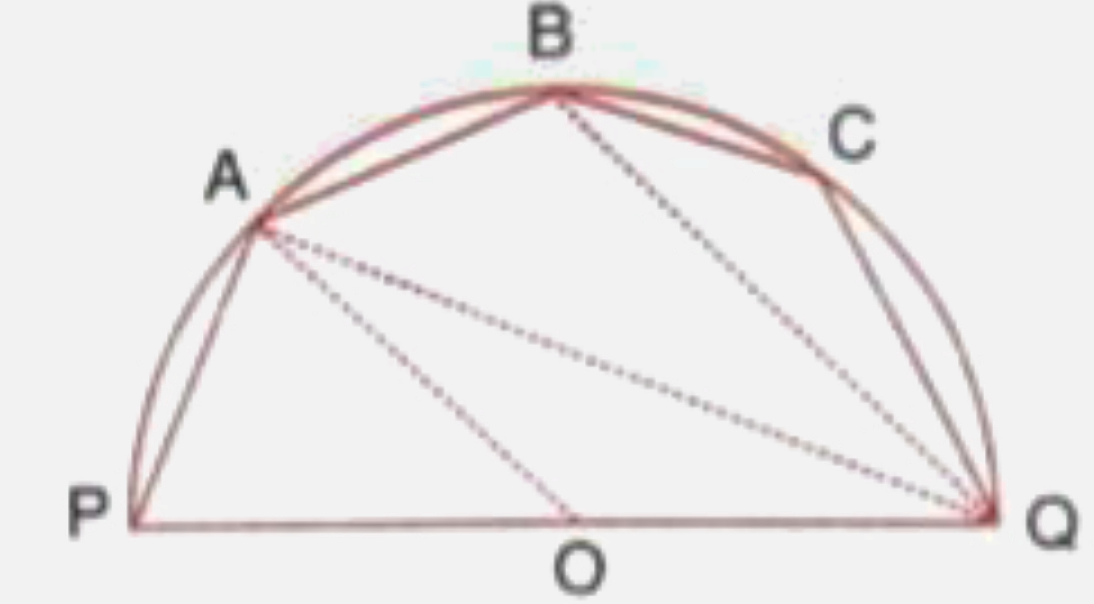 View Solution
View Solution

