State the inverse of the conditional given below :
" If it rains, then I shall not go out ".
To find the inverse of the given conditional statement "If it rains, then I shall not go out," we will follow these steps:
Step 1: Identify the components of the conditional statement
The statement can be broken down into two parts:
- Hypothesis (p): "It rains"
- Conclusion (q): "I shall not go out"
Step 2: Negate both the hypothesis and the conclusion
The inverse of a conditional statement is formed by negating both the hypothesis and the conclusion. Therefore, we need to negate p and q:
- Negation of p (not p): "It does not rain"
- Negation of q (not q): "I shall go out"
Step 3: Formulate the inverse statement
Now, we can combine the negated hypothesis and conclusion into the inverse statement:
- Inverse statement: "If it does not rain, then I shall go out."
Final Answer
The inverse of the conditional statement "If it rains, then I shall not go out" is:
"If it does not rain, then I shall go out."
---
The statement can be broken down into two parts:
- Hypothesis (p): "It rains"
- Conclusion (q): "I shall not go out"
The inverse of a conditional statement is formed by negating both the hypothesis and the conclusion. Therefore, we need to negate p and q:
- Negation of p (not p): "It does not rain"
- Negation of q (not q): "I shall go out"
Now, we can combine the negated hypothesis and conclusion into the inverse statement:
- Inverse statement: "If it does not rain, then I shall go out."
The inverse of the conditional statement "If it rains, then I shall not go out" is:
"If it does not rain, then I shall go out."
Similar Questions
State the contrapositive of the conditional given below :
" If it rains, then I shall not go out "
View SolutionNegation of the conditional ''If it rains, I shall go to school'' is
View SolutionWrite converse and inverse of the given conditional statement : If a number n is even, then n2 is even.
View SolutionWrite converse and inverse of the given conditional statement:
If a number IF is even , then n2 is even.
View SolutionState the converse, inverse and contrapositive of the conditional statement : 'If a sequence is bounded, then it is convergent.
View SolutionBromination of cyclohexene under conditions given below yields :

View SolutionCalculate the mean mark in the distribution given below:

Also, state the modal class.
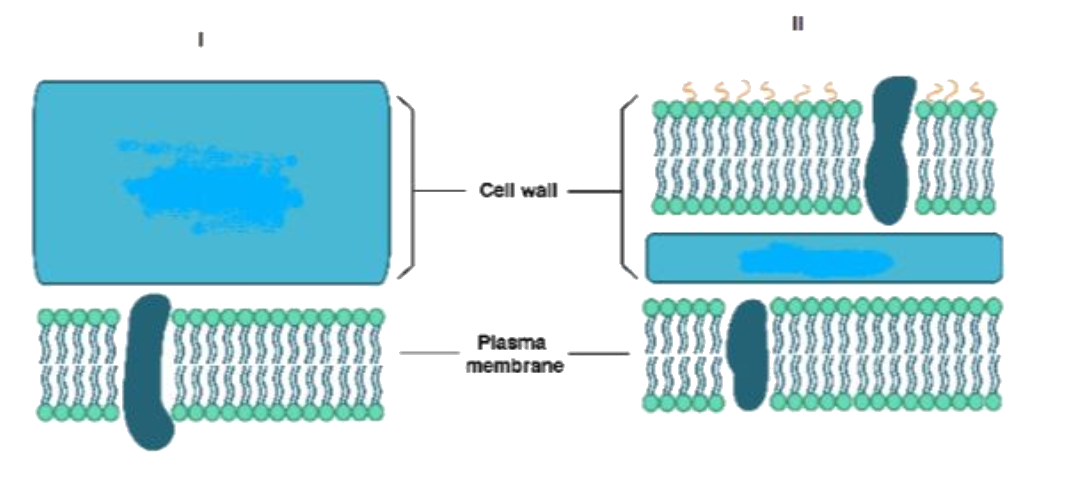
View SolutionIdentify I and II from the diagram given below.
View SolutionPick out lectin from those given below:
View SolutionFrom the diagram given below:
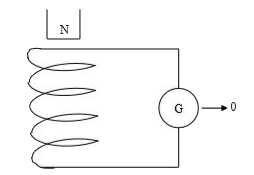
State the law which explains this observation.
View Solution
