ABCD is a parallelogram whose adjacent sides AB = 48 cm and BC = 14 cm . One of its diagonds AC = 50 cm . Find :
(i) the area of the parallelogram ABCD.
(ii) the distance between the longer sides.
(iii) the distance between the shorter sides.
The correct Answer is:=48 cm .
To solve the problem step by step, we will find the area of the parallelogram ABCD, the distance between the longer sides, and the distance between the shorter sides.
Step 1: Find the area of the parallelogram ABCD
1. Identify the sides and diagonal:
- AB = 48 cm
- BC = 14 cm
- AC (diagonal) = 50 cm
2. Calculate the semi-perimeter (s) of triangle ABC:
s=AB+BC+AC2=48+14+502=1122=56 cm
3. Use Heron's formula to find the area of triangle ABC:
- Area A of triangle ABC can be calculated using:
A=√s(s−a)(s−b)(s−c)
where a=AB=48, b=BC=14, and c=AC=50.
A=√56(56−48)(56−14)(56−50)
A=√56×8×42×6
4. Calculate the area:
- First, calculate the products:
56×8=448
42×6=252
A=√448×252
5. Finding the square root:
- Simplifying further:
A=√112896=336 cm2
6. Total area of parallelogram ABCD:
- Since the area of triangle ABC is equal to the area of triangle ADC, the total area of the parallelogram is:
Area of ABCD=2×336=672 cm2
Step 2: Find the distance between the longer sides (height from BC to AD)
1. Using the area formula for parallelogram:
Area=base×height
- Here, base = AB = 48 cm, and we need to find height h1:
672=48×h1
h1=67248=14 cm
Step 3: Find the distance between the shorter sides (height from AD to BC)
1. Using the area formula again:
- Here, base = BC = 14 cm, and we need to find height h2:
672=14×h2
h2=67214=48 cm
Final Answers:
(i) The area of the parallelogram ABCD is 672 cm².
(ii) The distance between the longer sides (height from BC to AD) is 14 cm.
(iii) The distance between the shorter sides (height from AD to BC) is 48 cm.
- AB = 48 cm
- BC = 14 cm
- AC (diagonal) = 50 cm
s=AB+BC+AC2=48+14+502=1122=56 cm
- Area A of triangle ABC can be calculated using:
A=√s(s−a)(s−b)(s−c)
where a=AB=48, b=BC=14, and c=AC=50.
A=√56(56−48)(56−14)(56−50)
A=√56×8×42×6
- First, calculate the products:
56×8=448
42×6=252
A=√448×252
- Simplifying further:
A=√112896=336 cm2
- Since the area of triangle ABC is equal to the area of triangle ADC, the total area of the parallelogram is:
Area of ABCD=2×336=672 cm2
Area=base×height
- Here, base = AB = 48 cm, and we need to find height h1:
672=48×h1
h1=67248=14 cm
- Here, base = BC = 14 cm, and we need to find height h2:
672=14×h2
h2=67214=48 cm
(i) The area of the parallelogram ABCD is 672 cm².
(ii) The distance between the longer sides (height from BC to AD) is 14 cm.
(iii) The distance between the shorter sides (height from AD to BC) is 48 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MENSURATIONEXERCISE - EXERCISE 23 A14videos
MENSURATION
- BOOK - ICSECHAPTER - MENSURATIONEXERCISE - EXERCISE 23 B1videos
MENSURATION
- BOOK - ICSECHAPTER - LINES AND ANGLESEXERCISE - Challenge2videos
LINES AND ANGLES
- BOOK - ICSECHAPTER - PERCENTAGE EXERCISE - EXERCISE 9C26videos
PERCENTAGE
Similar Questions
PQRS is a parallegoram whose adjecent sides PQ = 20 cm and QR = 21 cm one of its diagonals QS = 13 cm , find :
the area of the parallelogram PQRS.View SolutionABCD is a parallelogram having adjacent sides AB = 35 cm and BC = 28 cm . If the distance between its longer sides is 8 cm , find :
(i) the area of the parallelogram
(ii) the distance between its shorts sidesView SolutionThe adjacent sides of a parallelogram are 10 m and 8 m. If the distance between the longer sides is 4 m, find the distance between the shorter sides.
View SolutionPQRS is a parallegoram whose adjecent sides PQ = 20 cm and QR = 21 cm one of its diagonals PR = 13 cm , find :
the distance between the longer sides.View SolutionTwo adjacent sides of parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm, find the distance between shorter sides.
View SolutionIn parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
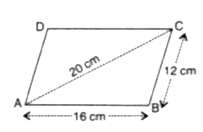 View Solution
View SolutionPQRS is a parallegoram whose adjecent sides PQ = 20 cm and QR = 21 cm one of its diagonals PR = 13 cm , find :
the distance between the shorter sides.View SolutionTwo adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long, Find the area of the parallelogram. Also, find the distance between shorter sides.
View SolutionThe adjacent sides of a parallelogram are 21 cm and 28 cm. If its one diagonal is 35 cm, find the area of the parallelogram.
View SolutionFind the perimeter and area of the given parallelogram ABCD. Also, find the distance between AD and BC.
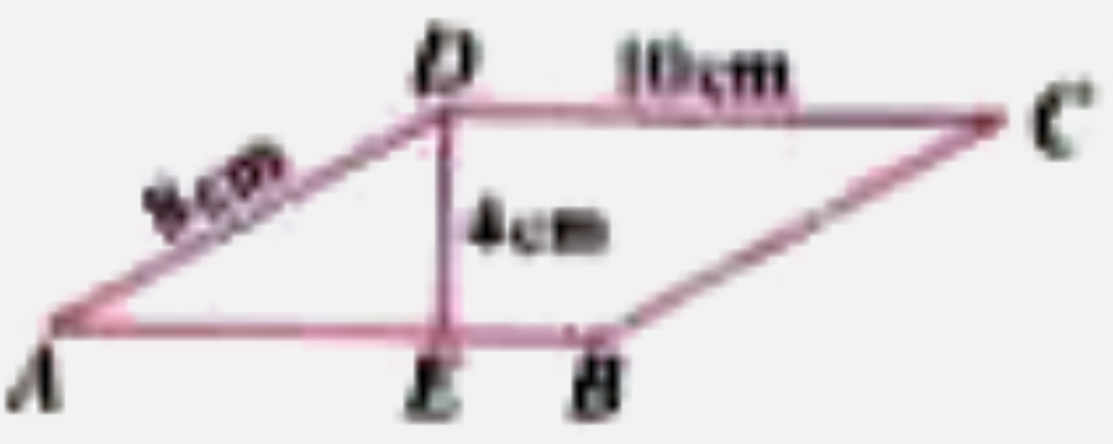 View Solution
View Solution

