Find the value of 2p2q−3pq2+2p−3p+1 when p=3,q=-3
To find the value of the expression 2p2q−3pq2+2p−3p+1 when p=3 and q=−3, we can follow these steps:
Step 1: Substitute the values of p and q into the expression.
The expression is:
2p2q−3pq2+2p−3p+1
Substituting p=3 and q=−3:
2(32)(−3)−3(3)(−32)+2(3)−3(3)+1
Step 2: Calculate 32 and −32.
Calculating 32:
32=9
Calculating −32:
−32=9
Step 3: Substitute the calculated values back into the expression.
Now substituting these values into the expression gives:
2(9)(−3)−3(3)(9)+2(3)−3(3)+1
Step 4: Calculate each term.
Calculating the first term:
2(9)(−3)=18×−3=−54
Calculating the second term:
−3(3)(9)=−27×9=−243
Calculating the third term:
2(3)=6
Calculating the fourth term:
−3(3)=−9
Step 5: Combine all the terms.
Now we combine all the terms:
−54−243+6−9+1
Step 6: Perform the addition and subtraction.
Calculating step by step:
−54−243=−297
−297+6=−291
−291−9=−300
−300+1=−299
Final Answer:
Thus, the value of the expression when p=3 and q=−3 is:
−299
The expression is:
2p2q−3pq2+2p−3p+1
Substituting p=3 and q=−3:
2(32)(−3)−3(3)(−32)+2(3)−3(3)+1
Calculating 32:
32=9
Calculating −32:
−32=9
Now substituting these values into the expression gives:
2(9)(−3)−3(3)(9)+2(3)−3(3)+1
Calculating the first term:
2(9)(−3)=18×−3=−54
Calculating the second term:
−3(3)(9)=−27×9=−243
Calculating the third term:
2(3)=6
Calculating the fourth term:
−3(3)=−9
Now we combine all the terms:
−54−243+6−9+1
Calculating step by step:
−54−243=−297
−297+6=−291
−291−9=−300
−300+1=−299
Thus, the value of the expression when p=3 and q=−3 is:
−299
Similar Questions
Find the value of :
2p + 3q + 4r + por when p =-1,q = 2 and r = 3
View SolutionFind the value of :
12p2×4p2q×(−3p)
View SolutionIf p = 3, q = 2 and r = -1, find the values of
2p2+3a2−r2+2pr−5pqr
View SolutionIf p = 3 , q = 2 and r = -1, find the values of
3p2q+5r2pq−3qr
View SolutionIf p = 4,q = -3 and r = 2, find the value of :p3+q3−r3−3pqr
View SolutionIf p = 4,q = 3 and r = -2, find the values of :
3pq+2qr2p+q−r
View SolutionFind the excess of 4p2−2pq+3q2 over 2p2−pq+4q2.
View SolutionIf p+1p+2=3, find the value of (p+2)3+1(p+2)3
View SolutionFind the value of p+q3 for given structure
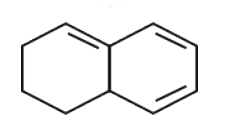
p = degree of unsturation (DU)
q = number of 2∘ carbon
View SolutionIf tanA+sinA=pandtanA−sinA=q, then the value of (p2−q2)2pq is :
View Solution
