In the given triangle, name the following:
(a). The vertices of the triangle
(b). The sides of the triangle
(c) the side opposite to vertex Q
(d) the vertex opposite to side PQ
(e) the three angles using three letters
(f) the three angles using a single letter
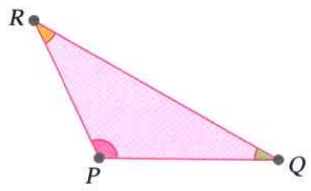
The correct Answer is:(a) P,Q,R
(b) PQ,QR,RP
(c) PR
(d) R
(e) ∠PQR,∠QRP,∠RPQ
(f) ∠P,∠Q,∠R.
Step by step video & image solution for In the given triangle, name the following: (a). The vertices of the triangle (b). The sides of the triangle (c) the side opposite to vertex Q (d) the vertex opposite to side PQ (e) the three angles using three letters (f) the three angles using a single letter by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - TRY THIS
24 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 12.1
7 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - REVISIONS EXERCISE
15 Videos
- SYMMETRYBOOK - ICSECHAPTER - SYMMETRYEXERCISE - Exercise 19B
13 Videos
- UNITARY METHODBOOK - ICSECHAPTER - UNITARY METHODEXERCISE - EXERCISE
16 Videos
Similar Questions
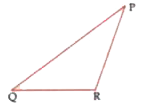
In the adjoining figure :
Name the vertex opposite to side PQ.
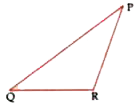
View SolutionIn the adjoining figure :
Name the side opposite the vertex Q.
View SolutionIn a triangle the greater angle has the longer side opposite to it.
View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View SolutionIf a vertex of an equilateral triangle is the origin and the side opposite to it has the equation x+y=1, then orthocentre of the triangle is :
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600 If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf one side of a triangle is double the other, and the angles on opposite sides differ by 600, then the triangle is equilateral (b) obtuse angled (c) right angled (d) acute angled
View SolutionProve that in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angles opposite to the first side is a right angle.
View SolutionProve that in a triangle if the square of one side is equal to the sum of the squares of the other two side then the angle opposite to the first side is a right angle.
View SolutionIf the square of one side of a triangle is equal to the sum of the squares of the other two sides then the triangle is a right triangle with the angle opposite the first sides as right angle.
View Solution
