The ratio of the load to the effort
To solve the question regarding the ratio of the load to the effort, we need to understand the basic concepts of levers and their components. Here’s a step-by-step solution:
Step 1: Understand the Components of a Lever
A lever consists of three main components:
- Fulcrum: The pivot point around which the lever rotates.
- Effort: The force applied to move the load.
- Load: The weight or resistance that needs to be moved.
Step 2: Identify the Distances
In a lever, there are two important distances:
- Effort Arm: The distance from the fulcrum to the point where the effort is applied.
- Load Arm: The distance from the fulcrum to the point where the load is applied.
Step 3: Define the Ratio
The ratio of the load to the effort can be expressed mathematically as:
Ratio=LoadEffort
Step 4: Calculate the Ratio
To find this ratio, you need to know the magnitudes of the load and the effort. If the load is represented by L and the effort by E, then:
Ratio=LE
Step 5: Conclusion
The ratio of the load to the effort helps us understand how much effort is required to lift a certain load using a lever. A higher ratio indicates that more effort is needed for the same load, while a lower ratio indicates that less effort is required.
A lever consists of three main components:
- Fulcrum: The pivot point around which the lever rotates.
- Effort: The force applied to move the load.
- Load: The weight or resistance that needs to be moved.
In a lever, there are two important distances:
- Effort Arm: The distance from the fulcrum to the point where the effort is applied.
- Load Arm: The distance from the fulcrum to the point where the load is applied.
The ratio of the load to the effort can be expressed mathematically as:
Ratio=LoadEffort
To find this ratio, you need to know the magnitudes of the load and the effort. If the load is represented by L and the effort by E, then:
Ratio=LE
The ratio of the load to the effort helps us understand how much effort is required to lift a certain load using a lever. A higher ratio indicates that more effort is needed for the same load, while a lower ratio indicates that less effort is required.
Topper's Solved these Questions
- ENERGY BOOK - ICSECHAPTER - ENERGY EXERCISE - Exercises Section I (Choose the correct option)
8 Videos
- ENERGY BOOK - ICSECHAPTER - ENERGY EXERCISE - Exercises Section I (Write T for True and F for False. Correct the False statements)
6 Videos
- ENERGY BOOK - ICSECHAPTER - ENERGY EXERCISE - Questions (Observe the figures and answer the questions)
6 Videos
- FORCEBOOK - ICSECHAPTER - FORCEEXERCISE - Picture Based Questions
2 Videos
Similar Questions
Mechanical advantage is less than 1 when the fulcrum is closer to the load than the effort.
View SolutionDraw a diagram of a block and tackle system of pulleys having a velocity ratio of 5. in your diagram indicate clearly the points of application and the directions of the load L and effort E. also mark the tension T in each strand.
View Solution
Knowledge Check
What is the ratio of load to effort in case of a tree house elevator shown in the diagram below?
 A1:1B2:1C1:2Dnone of the above
A1:1B2:1C1:2Dnone of the above
In a class two lever, the load arm is 80 cm long and the distance between the load and the effort is 120 cm. Find the MA.
View SolutionA lever of length 9 cm has its load arm 5 cm long and the effort arm is 9 cm long. (a) to which class does it belong ?
(b) Draw a diagram of the lever showing the position of the fulcrum F and directions of both the load L and effort E. (c) what is the mechanical advantage and velocity ratio if the efficiency is 100%?
(d) What will be the mechanical advantage and velocity ratio if the efficiency becomes 50%?
View SolutionIn Figure, draw a tackle to lift the load by applying the force in downward direction.
(a) Mark in the diagram the direction of load L and effort E.
(b) If the load is raised by 1 m, through what distance will the effot move ?
(c) State the number of strands of tackle supporting the load.
(d) What is the mechanical advantage of the system?
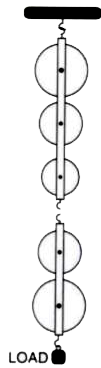
View SolutionA block and tackle system has V.R. = 5.
Draw a neat labelled diagram of a system indicating the direction of its load and effort.
View SolutionThe MA for a lever if the load is 150 N and the effort is 100 N is
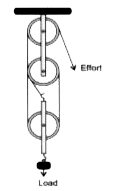
View SolutionDraw a diagram to show a block and tackle pulley system having a velocity ratio of 3 marking the direction of load (L), effort (E) and tension (T).
View Solution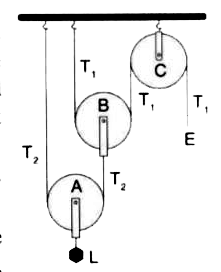
The diagram alongside shows an arrangement of three pulleys A,B and C. the load is marked as L and the effort as E.
(a) Name the pulleys A,B and C.
(b) Mark in the diagram the directions of load (L), effort (E) and tension T1andT2 in the two strings.
(c) How are the magnitudes of L and E related to the tension T1 ?
(d) Calculate mechanical advantage and velocity ratio of the arrangement.
(e) What assumptions have you made in parts (c) and (d) ?
View Solution