Name any two derived physical quantities
Step-by-Step Solution
1. Understanding Physical Quantities:
- Physical quantities are measurable attributes of physical phenomena. They can be expressed in numerical terms and have units associated with them.
2. Identifying Derived Physical Quantities:
- Derived physical quantities are those that are derived from fundamental physical quantities. Fundamental quantities are the basic building blocks of measurement, such as length, mass, time, electric current, temperature, amount of substance, and luminous intensity.
3. Example 1 - Area:
- Area is a derived physical quantity. It is calculated by multiplying length by length. The unit of area is square meters (m²) or square centimeters (cm²). Since length is a fundamental quantity, the area is derived from it.
4. Example 2 - Volume:
- Volume is another derived physical quantity. It is calculated by multiplying length by length by length (length × length × length). The unit of volume is cubic meters (m³) or cubic centimeters (cm³). Like area, volume is derived from the fundamental quantity of length.
5. Conclusion:
- Therefore, two examples of derived physical quantities are:
- Area (m² or cm²)
- Volume (m³ or cm³)
- Physical quantities are measurable attributes of physical phenomena. They can be expressed in numerical terms and have units associated with them.
- Derived physical quantities are those that are derived from fundamental physical quantities. Fundamental quantities are the basic building blocks of measurement, such as length, mass, time, electric current, temperature, amount of substance, and luminous intensity.
- Area is a derived physical quantity. It is calculated by multiplying length by length. The unit of area is square meters (m²) or square centimeters (cm²). Since length is a fundamental quantity, the area is derived from it.
- Volume is another derived physical quantity. It is calculated by multiplying length by length by length (length × length × length). The unit of volume is cubic meters (m³) or cubic centimeters (cm³). Like area, volume is derived from the fundamental quantity of length.
- Therefore, two examples of derived physical quantities are:
- Area (m² or cm²)
- Volume (m³ or cm³)
Topper's Solved these Questions
- PHYSICAL QUANTITIES AND MEASUREMENTBOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENTEXERCISE - EXERCISE (SECTION I) B. Choose the correct option
5 Videos
- PHYSICAL QUANTITIES AND MEASUREMENTBOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENTEXERCISE - EXERCISE (SECTION I) C. Write T for True and F for False. Correct the false statements.
5 Videos
- PHYSICAL QUANTITIES AND MEASUREMENTBOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENTEXERCISE - QUESTIONS
12 Videos
- MOTIONBOOK - ICSECHAPTER - MOTIONEXERCISE - TEST YOURSELF (NUMERICAL)
13 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - EXERCISES (PICTURE STUDY)
4 Videos
Similar Questions
Knowledge Check
Assertion: The units of some physical quantities can be expressed as combination of the base units. ltbr> Reason: We need only a limited number of units for expressing the derived physical quantities.
Aif both assertion and reason are true reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation fo assertion.CIf assertion is true but reaso is false.DIF both assertion and reason are false.
How do fundamental quantities differ from derived physical quantities?
View SolutionGive an example of two physical quantities such that their scalar product and vector product represent two different physical quantities .
View SolutionAssertion if two physical quantities have same dimension, then they can be certainly added or subtracted because
Reason if the dimension of both the quantities are same then both the physical quantities should be similar .
View SolutionName three physical quantities having the same dimensions.
View SolutionName three physical quantities without dimensions.
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionIn Column I physical quantities corresponding to hydrogen and hydrogen like atom are given. In column II, powers of principal quantum number n are givem on which thosee physical quantities depend. Match the two columns.
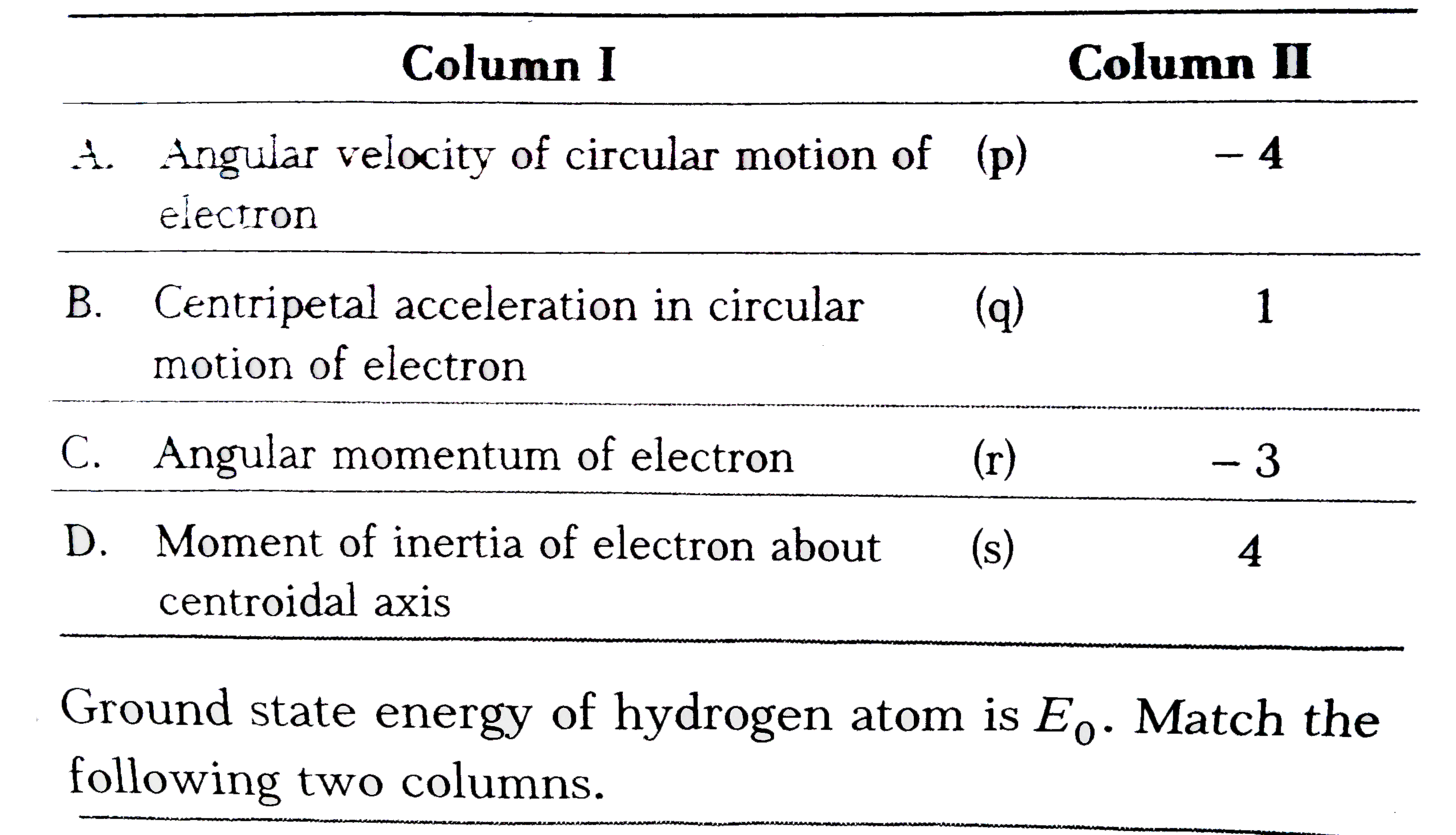
View Solution
