Calculate the pressure in the following cases :
(i) On the surface of a block , if it weighs 60 N and is lying on a side with area 0.3 m x 0.1 m.
(ii)On the same 60 N block , if it is lying on a side with area 0.1 m x 0.2 m .
To calculate the pressure in the given cases, we will use the formula for pressure:
Pressure(P)=Force(F)Area(A)
Where:
- Pressure is measured in Pascals (Pa)
- Force is measured in Newtons (N)
- Area is measured in square meters (m²)
Now, let's solve each case step by step.
Case (i):
1. Identify the given values:
- Weight of the block (Force, F) = 60 N
- Area (A) = 0.3 m × 0.1 m
2. Calculate the area:
A=0.3m×0.1m=0.03m2
3. Substitute the values into the pressure formula:
P=FA=60N0.03m2
4. Calculate the pressure:
P=2000Pa
Case (ii):
1. Identify the given values:
- Weight of the block (Force, F) = 60 N
- Area (A) = 0.1 m × 0.2 m
2. Calculate the area:
A=0.1m×0.2m=0.02m2
3. Substitute the values into the pressure formula:
P=FA=60N0.02m2
4. Calculate the pressure:
P=3000Pa
Summary of Results:
- Pressure in Case (i) = 2000 Pa
- Pressure in Case (ii) = 3000 Pa
- Pressure is measured in Pascals (Pa)
- Force is measured in Newtons (N)
- Area is measured in square meters (m²)
1. Identify the given values:
- Weight of the block (Force, F) = 60 N
- Area (A) = 0.3 m × 0.1 m
A=0.3m×0.1m=0.03m2
P=FA=60N0.03m2
P=2000Pa
1. Identify the given values:
- Weight of the block (Force, F) = 60 N
- Area (A) = 0.1 m × 0.2 m
A=0.1m×0.2m=0.02m2
P=FA=60N0.02m2
P=3000Pa
- Pressure in Case (i) = 2000 Pa
- Pressure in Case (ii) = 3000 Pa
Topper's Solved these Questions
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Questions (Choose the correct option to fill in the blank)
8 Videos
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - Exercises (Section I) Name the following
6 Videos
- FORCE AND PRESSURE BOOK - ICSECHAPTER - FORCE AND PRESSURE EXERCISE - EXERCISE 3.3 (STUDY QUESTIONS)
9 Videos
- ENERGYBOOK - ICSECHAPTER - ENERGYEXERCISE - THEME ASSIGNMENT
4 Videos
- HEAT TRANSFER BOOK - ICSECHAPTER - HEAT TRANSFER EXERCISE - Picture Study
2 Videos
Similar Questions
The surface tension of liquid is 0.5 N / m . If a film is held on a ring of area 0.02 m square , its surface energy is
View SolutionA block of iron has dimensions 2 m x 0.5 m x 0.25 m. The density of iron is 7.8gcm−3 . Find the mass of block.
View SolutionThe shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
View SolutionA uniform square block of side 'a' and mass 'm' is lying on a horizontal surface. A small block of mass m is placed on the top block. Find the distance by which normal reaction is shifted.
View SolutionA block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?
View SolutionA stone of weight of 2 kgf is lying on the roof of a building 60 m high. Calculate the amount of stored energy in the stone. [Take 1 kgf=10N]
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and g=10ms−2 The frictional force on the block is
View SolutionA block of mass M slides along the sides of bowl as shown in the figure. The walls of the bowl are frictionless and the base has coefficient of friction 0.1, and length 0.5m. The block is released from the point A which is 0.2 m high as shown in figure. Then the block comes to rest
View SolutionTwo parallel side of a trapezium are 60cm and 77cm and other sides are 25cm and 26cm. Find the area of the trapezium.
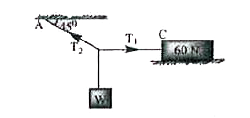
View SolutionIn the figure, a block of weight 60N is placed on a rough surface. The coefficient of friction between the block and the surface is 0.5. The minimum weight of the block does not slip on the surface is (x×10)N. The value of x is
View Solution
