Work done = Force/Distance
To determine whether the statement "Work done = Force/Distance" is correct or not, we will derive the correct relationship between work done, force, and distance.
1. Understanding Work Done:
Work done (W) is defined as the product of the force (F) applied to an object and the distance (S) over which that force is applied in the direction of the force. The formula for work done is:
W=F×S
2. Newton's Second Law:
According to Newton's second law of motion, force is defined as the product of mass (m) and acceleration (a):
F=m×a
3. Kinematic Equation:
We can use the kinematic equation that relates initial velocity (u), final velocity (v), acceleration (a), and distance (S):
v2=u2+2aS
4. Multiplying by Mass:
To relate this to energy, we multiply the entire equation by mass (m):
mv2=mu2+2maS
5. Dividing by 2:
Dividing the entire equation by 2 gives us:
12mv2=12mu2+maS
6. Relating to Kinetic Energy:
We know that kinetic energy (K.E.) is given by:
K.E.=12mv2
Therefore, we can rewrite the equation as:
K.E.final−K.E.initial=maS
7. Substituting Force:
Since F=ma, we can substitute this into our equation:
K.E.final−K.E.initial=F×S
8. Conclusion:
The change in kinetic energy (ΔK) is equal to the work done (W):
ΔK=W
Thus, we conclude that:
W=F×S
Therefore, the statement "Work done = Force/Distance" is incorrect. The correct relationship is:
W=F×S
Final Answer:
The statement "Work done = Force/Distance" is false. The correct formula is:
W=F×S
Work done (W) is defined as the product of the force (F) applied to an object and the distance (S) over which that force is applied in the direction of the force. The formula for work done is:
W=F×S
According to Newton's second law of motion, force is defined as the product of mass (m) and acceleration (a):
F=m×a
We can use the kinematic equation that relates initial velocity (u), final velocity (v), acceleration (a), and distance (S):
v2=u2+2aS
To relate this to energy, we multiply the entire equation by mass (m):
mv2=mu2+2maS
Dividing the entire equation by 2 gives us:
12mv2=12mu2+maS
We know that kinetic energy (K.E.) is given by:
K.E.=12mv2
Therefore, we can rewrite the equation as:
K.E.final−K.E.initial=maS
Since F=ma, we can substitute this into our equation:
K.E.final−K.E.initial=F×S
The change in kinetic energy (ΔK) is equal to the work done (W):
ΔK=W
Thus, we conclude that:
W=F×S
Therefore, the statement "Work done = Force/Distance" is incorrect. The correct relationship is:
W=F×S
The statement "Work done = Force/Distance" is false. The correct formula is:
W=F×S
Topper's Solved these Questions
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Questions (Choose the correct option to fill in the blank)
5 Videos
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Exercises (Name the following)
8 Videos
- WORK AND ENERGYBOOK - ICSECHAPTER - WORK AND ENERGYEXERCISE - Picture Study
3 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - Picture Study
4 Videos
Similar Questions
Knowledge Check
Assertion , No work is done if the displacement is zero
Reason: Work done by the force is defined to be the product of component of the force in the the direction of the displacement and the magnitude of displacement.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true not but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.Work done = force × ………..
AdistanceBvelocityCtimeDdisplacementWork done by buoyant force is .......
ApositiveBnegativeCzeroDcannot definitely say
A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is
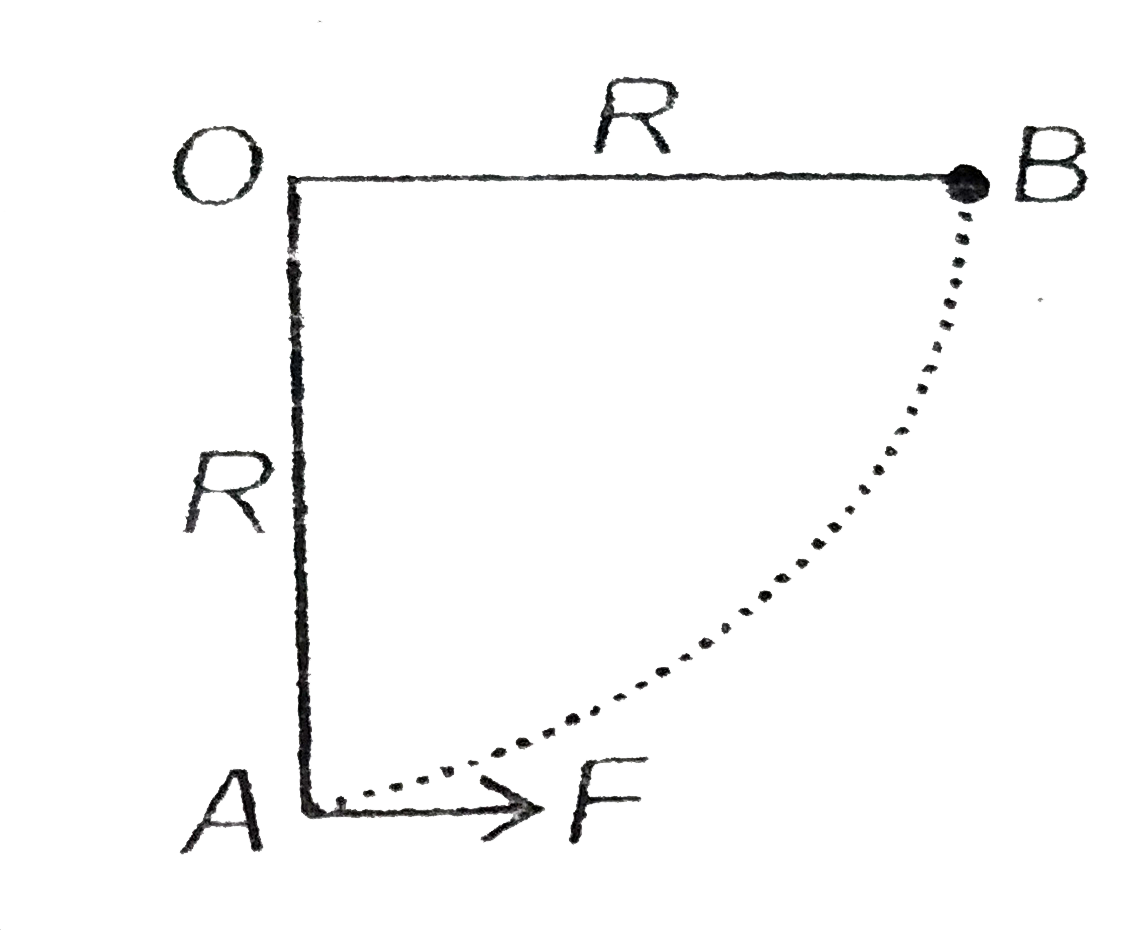
View SolutionWork done by an individual force is zero if the work done by the resultant force is also zero.
View SolutionWhen is the work done by a force is positive and when is it negative ?
View SolutionA force F acting on an object varies with distance x
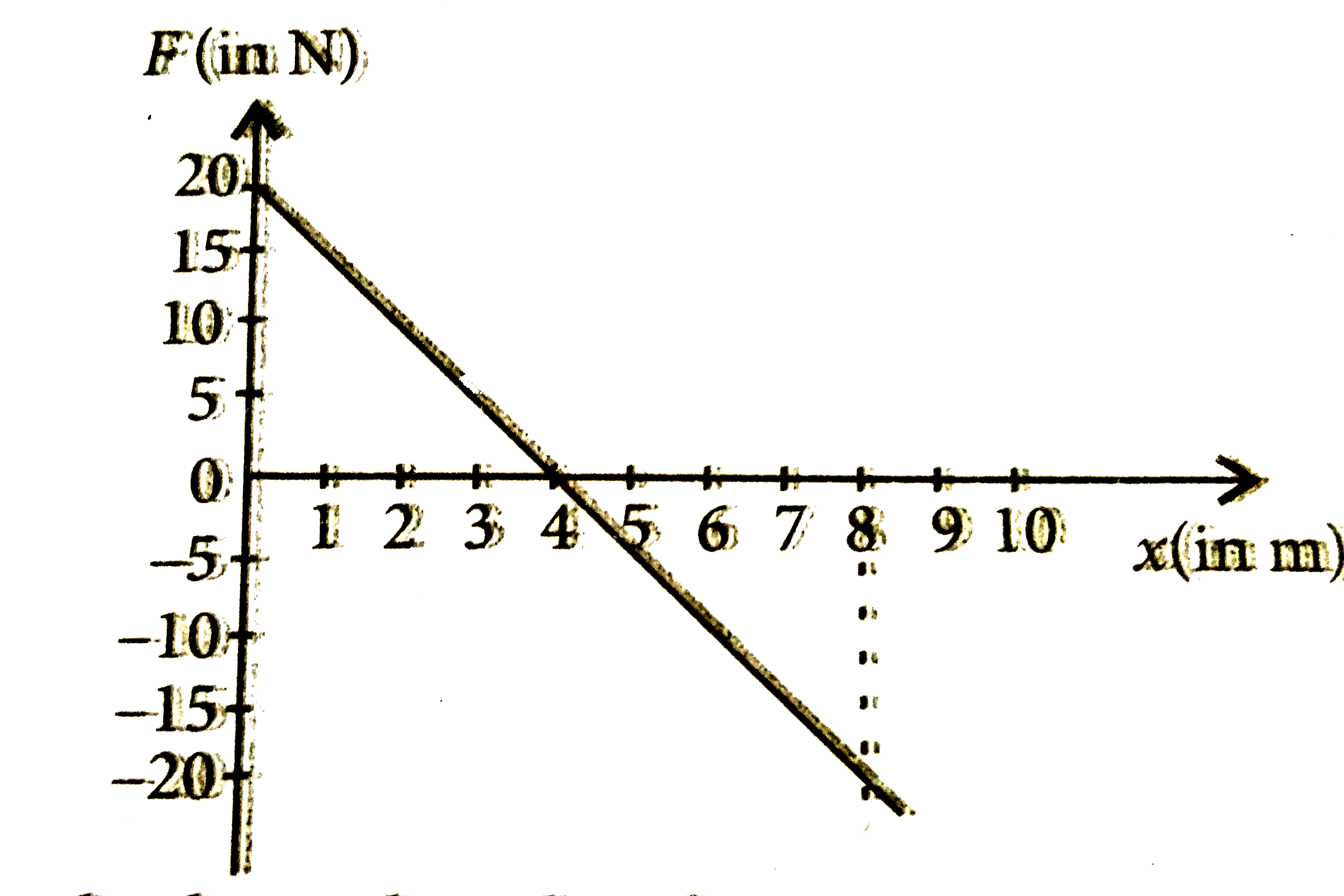
The work done by the force in moving the object from x=0 to x=8 m is
View SolutionA force F acting on an object varies with distance x as shown in the figure. The work done by the force in moving the object from x=0 to x = 20 m is
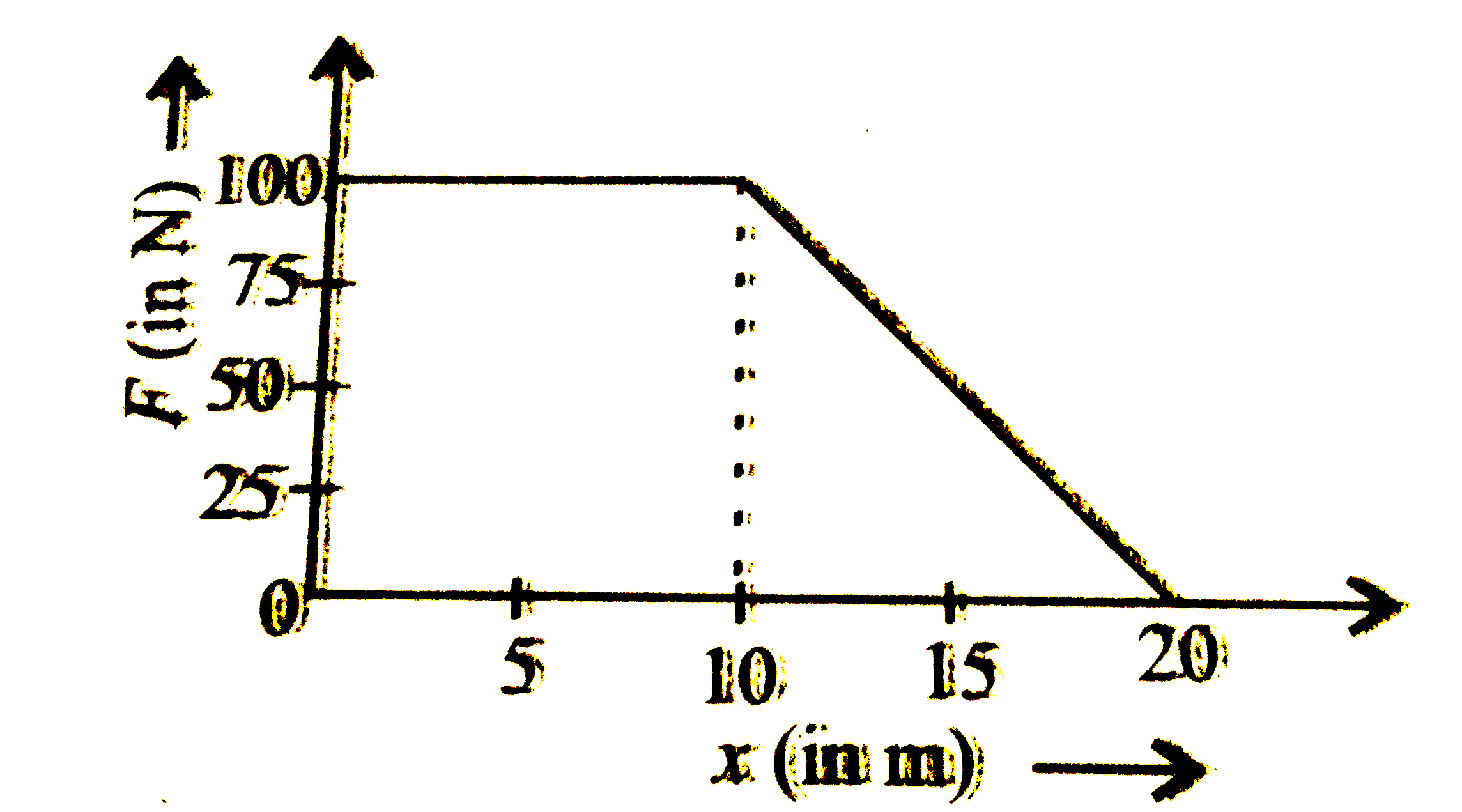
View Solution
