The atomic radius of an ion which crystallizes in fcc structure is 97 Å. Calculate the lattice constant.
The correct Answer is:a=3.6×10−10 m
Atomic radius, r=97Å=97×10−10 m.
For fcc structure, r=a/(2√2) or lattice constant, = 97×10−10m×2×1.4142=3.6×10−10 m.
Topper's Solved these Questions
- SOLID STATEBOOK - KALYANI PUBLICATIONCHAPTER - SOLID STATEEXERCISE - FOLLOW UP PROBLEMS(Type 1. Calculation of Density of unit cell.)
2 Videos
- SOLID STATEBOOK - KALYANI PUBLICATIONCHAPTER - SOLID STATEEXERCISE - FOLLOW UP PROBLEMS(Type II. Calculation of Edge length, Interionic distances and volume of Unit cell.)
4 Videos
- SOLID STATEBOOK - KALYANI PUBLICATIONCHAPTER - SOLID STATEEXERCISE - INTEXT QUESTIONS
18 Videos
- POLYMERS BOOK - KALYANI PUBLICATIONCHAPTER - POLYMERS EXERCISE - EXERCISE (PART-II (DESCRIPTIVE QUESTIONS )) ( SHORT ANSWER QUESTIONS
5 Videos
- SURFACE CHEMISTRY BOOK - KALYANI PUBLICATIONCHAPTER - SURFACE CHEMISTRY EXERCISE - EXERCISE (PART-II ( DESCRIPTIVE QUESTIONS )) (VERY SHORT ANSWER QUESTIONS)
31 Videos
Similar Questions
Knowledge Check
If an atom crystallizes in bcc lattice with r=4Å then the edge length will be
A2ÅB8ÅC2.39ÅD9.23ÅIf the lattice parameter for a crystalline structure is 3.6Å, then the atomic radius is fcc crystals is
A1.81ÅB2.10ÅC2.92ÅD1.27ÅIf the lattice parameter for a crystalline structure is 3.6Å, then the atomic radius of fcc crystals is
A1.27AB1.81AC2.10AD2.92A
The radius of chromium atom is 1.25Å. If it crystallises in body centred cubic lattice, calculate the length of the edge of the unit cell.
View SolutionIf the lattice parameter for a crystalline structure is 3.6Å, then the atomic radius is fcc crystals is
View SolutionIf the radius of a metal is 2.00Å and its crystal structure is in cubic close packed (fc lattice), what is the volume (∈cm3) of one unit cell?
View SolutionIce crystallizes in a hexagonal lattice. At the low temperature at which the structure was determined, the lattice constants were a=4.53Å and c=7.41Å (as shown in fig.) How many H2O molecules are contained in a unit cell ? (Density of ice =0.92gm/cc)
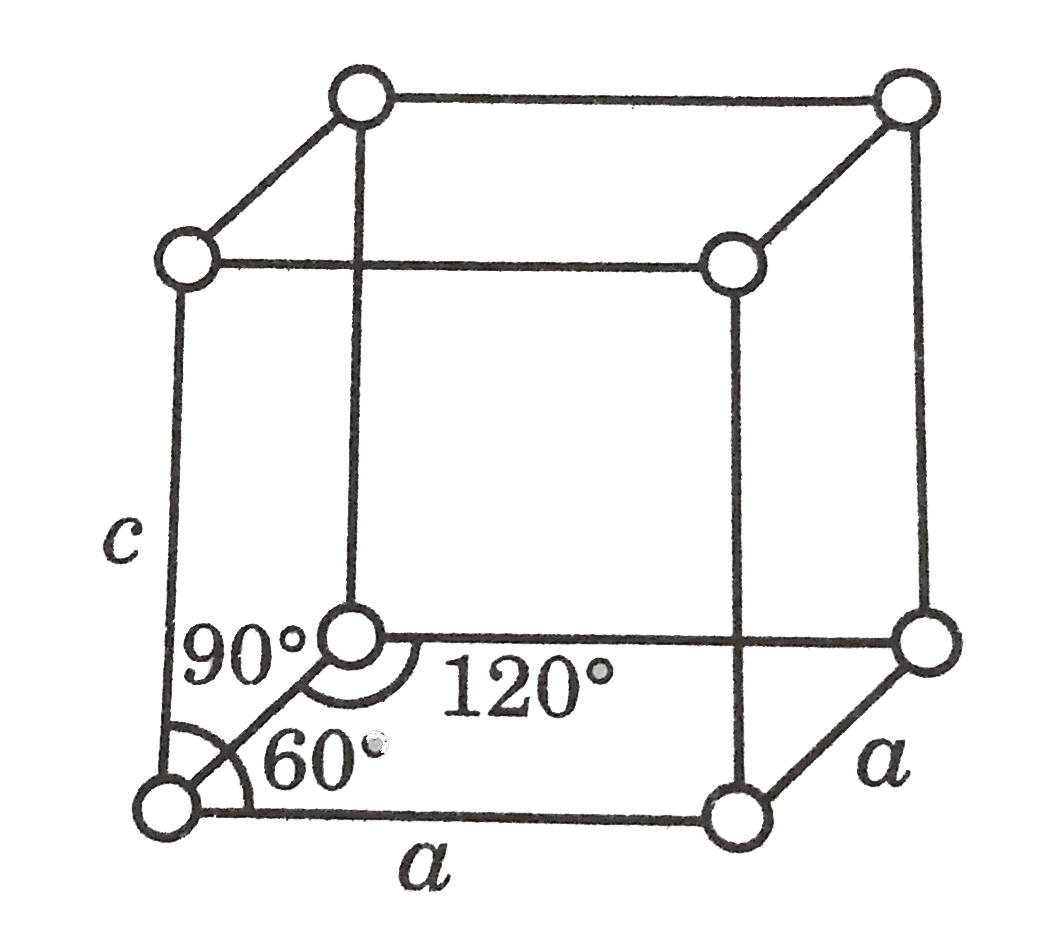
View SolutionIce crystallizes in a hexagonal lattice. At the low temperature at which the structure was determined, the lattice constants were a=4.53Åandc=7.41Å (as shown in fig). How mant H2O molecules are contained in a unit cell ? (Density of ice = 0.92 gm/cc)

View Solution
