Draw any polygon and divide it into triangular parts. Work out the sum of interior angles of the polygon.
To solve the problem of finding the sum of the interior angles of a polygon, let's follow these steps:
Step 1: Draw a Polygon
- Draw a polygon with 5 sides (a pentagon). Label the vertices as A, B, C, D, and E.
Step 2: Divide the Polygon into Triangles
- To divide the polygon into triangles, draw diagonals from one vertex to the non-adjacent vertices. For example, draw diagonals from vertex A to vertices C and D. This will create three triangles:
- Triangle ABC
- Triangle ACD
- Triangle ADE
Step 3: Count the Number of Triangles
- In the case of a pentagon (5-sided polygon), we have formed 3 triangles by drawing the diagonals.
Step 4: Calculate the Sum of Interior Angles of Each Triangle
- The sum of the interior angles of each triangle is always 180 degrees. Therefore, for 3 triangles:
- Sum of angles = 3 triangles × 180 degrees/triangle = 540 degrees.
Step 5: Write the Sum of the Interior Angles of the Polygon
- The sum of the interior angles of the polygon (pentagon) is 540 degrees. This can be represented as:
- Angle A + Angle B + Angle C + Angle D + Angle E = 540 degrees.
Final Answer
- The sum of the interior angles of the polygon is 540 degrees.
---
- Draw a polygon with 5 sides (a pentagon). Label the vertices as A, B, C, D, and E.
- To divide the polygon into triangles, draw diagonals from one vertex to the non-adjacent vertices. For example, draw diagonals from vertex A to vertices C and D. This will create three triangles:
- Triangle ABC
- Triangle ACD
- Triangle ADE
- In the case of a pentagon (5-sided polygon), we have formed 3 triangles by drawing the diagonals.
- The sum of the interior angles of each triangle is always 180 degrees. Therefore, for 3 triangles:
- Sum of angles = 3 triangles × 180 degrees/triangle = 540 degrees.
- The sum of the interior angles of the polygon (pentagon) is 540 degrees. This can be represented as:
- Angle A + Angle B + Angle C + Angle D + Angle E = 540 degrees.
- The sum of the interior angles of the polygon is 540 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Some of the interior angle of the polygon is
A(n−4)90∘B(2n−4)180∘C(2n−4)90∘D(n−4)180∘Find the sum of the interior angles of the polygon given below .
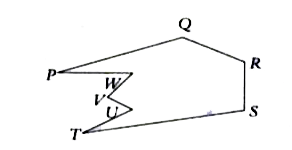 A1080∘B1440∘C1800∘D900∘
A1080∘B1440∘C1800∘D900∘
Find the sum of the interior angles of a polygon of 8 sides.
View SolutionFind the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of the an 8-sided polygon.
View SolutionFind the sum of the interior angles of the polygon gives below.
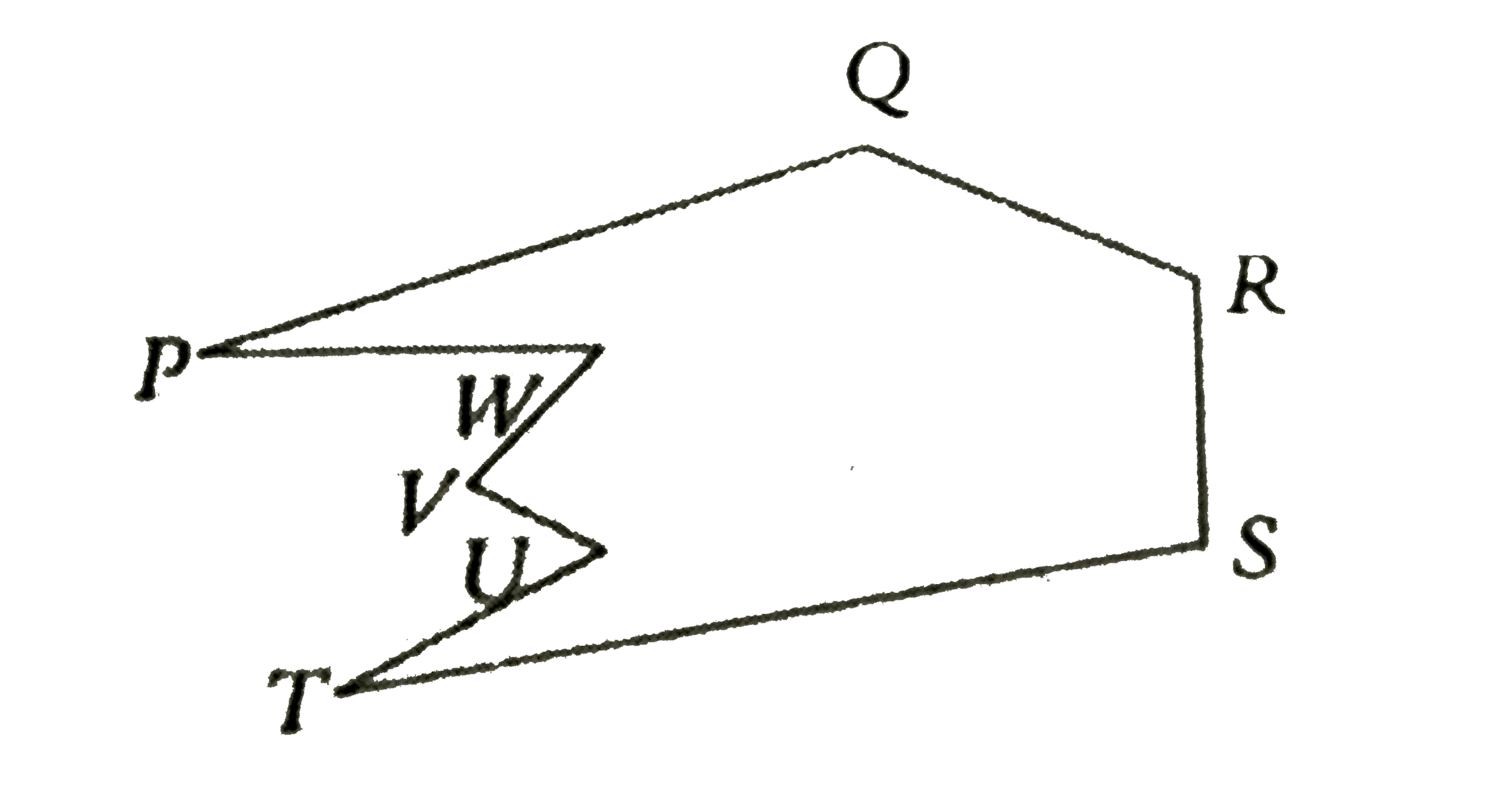
View SolutionIn an n-sided regular polygon, each exterior angle is 72∘. Find the sum of all the interior angles of the polygon.
View SolutionIn an n-sided regular polygon, each exterior angle is 72∘. Find the sum of all the interior angles of the polygon.
View Solution