Question

The radius of an octahedral void is 'r' and the radius of an atom is 'R' when these are in close packing. Derive the relation between the two.

Explanation

To derive the relation between the radius of an octahedral void (r) and the radius of an atom (R) in close packing, we can follow these steps:

Step 1: Understanding the Octahedral Void
In a close-packed structure, an octahedral void is formed when atoms are arranged in a specific geometric configuration. An octahedral void is surrounded by six atoms.

Step 2: Visualizing the Unit Cell
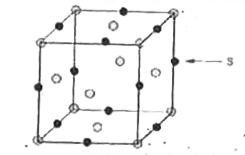
Consider a cubic unit cell where atoms are located at the corners and the center of the cube. The length of the unit cell is denoted as 'a'.

Step 3: Determining the Diagonal of the Cube
In a cube, the diagonal (AC) can be calculated using the Pythagorean theorem. For a cube with side length 'a':
- The diagonal AC can be calculated as:
\( AC = \sqrt{AB^2 + BC^2} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2} \)

Step 4: Relating the Lengths to the Radii
In the context of the octahedral void:
- The distance AC is equal to the sum of the diameters of the spheres (atoms) that surround the void. Since there are two spheres contributing to the distance from the center of the void to the edge, we have:
\( AC = 2R + 2r \)
where R is the radius of the atom and r is the radius of the octahedral void.

Step 5: Setting Up the Equation
From the previous steps, we have:
\( a\sqrt{2} = 2R + 2r \)

Step 6: Solving for r
Rearranging the equation gives:
\( 2r = a\sqrt{2} - 2R \)
Dividing through by 2:
\( r = \frac{a\sqrt{2}}{2} - R \)

Step 7: Expressing in Terms of R
To find the relationship between r and R, we need to express 'a' in terms of R. In a close-packed structure, the relationship between the radius of the atom (R) and the edge length (a) is:
\( a = 2R \)
Substituting this into the equation for r:
\( r = \frac{(2R)\sqrt{2}}{2} - R \)
This simplifies to:
\( r = R\sqrt{2} - R \)
Factoring out R gives:
\( r = R(\sqrt{2} - 1) \)

Final Relation
Thus, the final relation between the radius of the octahedral void (r) and the radius of the atom (R) is:
\( r = R(\sqrt{2} - 1) \approx 0.414R \)