Define solubility product.
Step-by-Step Solution:
1. Definition of Solubility Product (Ksp):
- The solubility product, denoted as Ksp, is defined as the equilibrium constant for the dissolution of a sparingly soluble ionic compound in water. It represents the extent to which a solid solute dissolves to form a saturated solution.
2. Understanding the Concept of Equilibrium:
- In a saturated solution, the rate of dissolution of the solid is equal to the rate of precipitation of the solid from the solution. This establishes an equilibrium between the solid and its ions in solution.
3. General Expression for Ksp:
- For a general ionic compound represented by the formula AB that dissociates into A+ and B− ions, the dissolution can be represented as:
AB(s)⇌A+(aq)+B−(aq)
- The solubility product expression is given by:
Ksp=(A+)(B−)
- Here, (A+) and (B−) are the molar concentrations of the ions at equilibrium.
4. Example of Ksp Calculation:
- Consider the dissolution of barium sulfate (BaSO4):
BaSO4(s)⇌Ba2+(aq)+SO42−(aq)
- The Ksp expression for barium sulfate would be:
Ksp=(Ba2+)(SO42−)
5. Conditions for Solubility:
- Solubility can be categorized based on the concentration of the solute:
- Soluble: Greater than 0.1 M
- Slightly Soluble: Between 0.01 M and 0.1 M
- Sparingly Soluble: Less than 0.01 M
6. Conclusion:
- The solubility product is crucial for understanding the solubility of ionic compounds and predicting whether a precipitate will form in a solution.
---
- The solubility product, denoted as Ksp, is defined as the equilibrium constant for the dissolution of a sparingly soluble ionic compound in water. It represents the extent to which a solid solute dissolves to form a saturated solution.
- In a saturated solution, the rate of dissolution of the solid is equal to the rate of precipitation of the solid from the solution. This establishes an equilibrium between the solid and its ions in solution.
- For a general ionic compound represented by the formula AB that dissociates into A+ and B− ions, the dissolution can be represented as:
AB(s)⇌A+(aq)+B−(aq)
- The solubility product expression is given by:
Ksp=(A+)(B−)
- Here, (A+) and (B−) are the molar concentrations of the ions at equilibrium.
- Consider the dissolution of barium sulfate (BaSO4):
BaSO4(s)⇌Ba2+(aq)+SO42−(aq)
- The Ksp expression for barium sulfate would be:
Ksp=(Ba2+)(SO42−)
- Solubility can be categorized based on the concentration of the solute:
- Soluble: Greater than 0.1 M
- Slightly Soluble: Between 0.01 M and 0.1 M
- Sparingly Soluble: Less than 0.01 M
- The solubility product is crucial for understanding the solubility of ionic compounds and predicting whether a precipitate will form in a solution.
Topper's Solved these Questions
- EQUILIBRIUM BOOK - ICSECHAPTER - EQUILIBRIUM EXERCISE - OBJECTIVE (MULTIPLE CHOICE ) TYPE QUESTIONS
114 Videos
- EQUILIBRIUM BOOK - ICSECHAPTER - EQUILIBRIUM EXERCISE - TRUE OR FALSE TYPE QUESTION
22 Videos
- EQUILIBRIUM BOOK - ICSECHAPTER - EQUILIBRIUM EXERCISE - SHORT ANSWER TYPE QUESTIONS
44 Videos
- ENVIRONMENTAL CHEMISTRY BOOK - ICSECHAPTER - ENVIRONMENTAL CHEMISTRY EXERCISE - NCERT TEXT-BOOK EXERCISE
20 Videos
- HYDROCARBONS BOOK - ICSECHAPTER - HYDROCARBONS EXERCISE - NCERT TEXT-BOOK EXERCISES
46 Videos
Similar Questions
Knowledge Check
Which of the following is not an application of solubility product ?
APredicting precipitation formationBPredicting solubility of sparingly soluble saltCPredicting pH of a buffer solutionDQualitative analysisFor a sparingly soluble salt ApBq, the relationship of its solubility product (Ks) with its solubility (S) is
AKs=Sp+q.Pp.qqBKs=Sp+q.Pq.qpCKs=Spq.pp.qqDKs=Spq,(pq)p+q
The solubility of electrolytes MX1,MX2andMX3is1×10−3 moles per litre. Hence their respective solubility products are :
View SolutionSTATEMENT-1: Sparingly soluble salts AB and XY2 with the same solubility product, will have different solubility.
STATEMENT-2: Solubiluty of sparingly soluble salt depend upon solubility product.
View SolutionThe stoichiometre and solubility product oFIGURE a salt with the solubility curve given below is respectively.
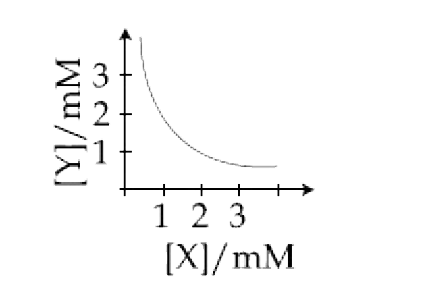
View SolutionIf the solubility of Al2(SO4)3 is S , then its solubility product is
View SolutionA precipitate is formed when ionic product becomes equal to the solubility product.
View SolutionWhich one has the minimum solubility product ?
View Solution
