In each of the following the co-ordinates of the three vertices of a rectangle ABCD are given. By plotting the given points, find, in each case, the co-ordinates of the fourth vertex:
A(2,0),B(8,0) and C(8,4)
The correct Answer is:(2,4)
To find the coordinates of the fourth vertex D of the rectangle ABCD given the coordinates of points A, B, and C, we can follow these steps:
Step 1: Plot the Given Points
We have the following coordinates:
- A(2, 0)
- B(8, 0)
- C(8, 4)
Plot these points on a Cartesian plane:
- Point A is at (2, 0), which is 2 units to the right of the origin on the x-axis.
- Point B is at (8, 0), which is 8 units to the right of the origin on the x-axis.
- Point C is at (8, 4), which is 8 units to the right and 4 units up from the origin.
Step 2: Identify the Rectangle's Structure
From the plotted points:
- Points A and B are on the same horizontal line (y = 0), indicating that they are on the base of the rectangle.
- Point C is directly above point B, which indicates that the rectangle's height extends vertically from point B to point C.
Step 3: Determine the Fourth Vertex D
Since ABCD is a rectangle, the opposite sides are equal and parallel. We can find the coordinates of point D by observing that:
- The x-coordinate of D will be the same as that of A (since D is vertically aligned with A).
- The y-coordinate of D will be the same as that of C (since D is horizontally aligned with C).
Thus, the coordinates of point D will be:
- D(2, 4)
Step 4: Finalize the Coordinates
The coordinates of the fourth vertex D of the rectangle ABCD are:
- D(2, 4)
Summary
The coordinates of the fourth vertex D are (2, 4).
---
We have the following coordinates:
- A(2, 0)
- B(8, 0)
- C(8, 4)
- Point A is at (2, 0), which is 2 units to the right of the origin on the x-axis.
- Point B is at (8, 0), which is 8 units to the right of the origin on the x-axis.
- Point C is at (8, 4), which is 8 units to the right and 4 units up from the origin.
From the plotted points:
- Points A and B are on the same horizontal line (y = 0), indicating that they are on the base of the rectangle.
- Point C is directly above point B, which indicates that the rectangle's height extends vertically from point B to point C.
Since ABCD is a rectangle, the opposite sides are equal and parallel. We can find the coordinates of point D by observing that:
- The x-coordinate of D will be the same as that of A (since D is vertically aligned with A).
- The y-coordinate of D will be the same as that of C (since D is horizontally aligned with C).
- D(2, 4)
The coordinates of the fourth vertex D of the rectangle ABCD are:
- D(2, 4)
The coordinates of the fourth vertex D are (2, 4).
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CO-ORDINATE GEOMETRYEXERCISE - EXERCISE 26(B)46videos
CO-ORDINATE GEOMETRY
- BOOK - ICSECHAPTER - CO-ORDINATE GEOMETRYEXERCISE - EXERCISE 26(C)35videos
CO-ORDINATE GEOMETRY
- BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-225videos
CIRCLES
- BOOK - ICSECHAPTER - COMPLEMENTARY ANGLESEXERCISE - EXERCISE64videos
COMPLEMENTARY ANGLES
Similar Questions
In each of the following the co-ordinates of the three vertices of a rectangle ABCD are given. By plotting the given points, find, in each case, the co-ordinates of the fourth vertex:
A(-4,-6),C(6,0) and D(-4,0)View SolutionIn each of the following the co-ordinates of the three vertices of a rectangle ABCD are given. By plotting the given points, find, in each case, the co-ordinates of the fourth vertex:
A(4,2), B(-2,2) and D(4,-2)View SolutionIn each of the following the co-ordinates of the three vertices of a rectangle ABCD are given. By plotting the given points, find, in each case, the co-ordinates of the fourth vertex:
B(10,4),C(0,4) and D(0,-2)View SolutionA(−2,2),B(8,2) and C(4,−4) are the vertice of a parallelogram ABCD. By plotting the given points on a graph paper, find the co-ordinates of the fourth vertex D.
View SolutionFrom the given figure, find :
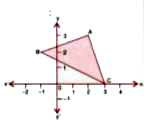
the co ordinates of A, B and C.View SolutionThe co-ordinates of two vertices of ΔABC are A(8,-9,8) and B(1,2,3). The medians of the triangle meet at the point (5,-2,4). Find the co-ordinates of the vertex C.
View SolutionTwo vertices of a ΔABC are given by A(6,4)andB(−2,2) and its centroid is G (3,4). Find the co-ordinates of the vertex C of ΔABC.
View SolutionThe co-ordinates of the vertices of a ΔABC are A(1,0),B(3,6)andC(3,2). Find the length of its medians.
View SolutionIf the three vertices of a parallelogram ABCD are
A(3, -1, 5), B(1, -2, -4) and C(0, 3, 0), then the
coordinates of fourth vertex isView SolutionThree vertices of a parallelogram ABCD are A(3, 1, 2), B(0, 1, 5) and C(-1, 2, -3) Find the
coordinates of the fourth vertex.View Solution

