An object of length 4 cm is placed in front of a concave mirror at distance 30 cm. The focal length of mirror is 15 cm. a. Where will the image form? B. What will be the length of image?
The correct Answer is:a. 30 cm in front of mirror, b. 4 cm
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the given values
- Length of the object (h_o) = 4 cm
- Object distance (u) = -30 cm (negative due to sign convention)
- Focal length (f) = -15 cm (negative for concave mirror)
Step 2: Use the mirror formula to find the image distance (v)
The mirror formula is given by:
1v+1u=1f
Substituting the values:
1v+1−30=1−15
Step 3: Rearranging the equation
Rearranging gives:
1v=1−15+130
Step 4: Find a common denominator
The common denominator for -15 and 30 is 30:
1−15=−230
So,
1v=−230+130=−2+130=−130
Step 5: Solve for v
Taking the reciprocal gives:
v=−30cm
Step 6: Interpret the result
The negative sign indicates that the image is formed in front of the mirror, at a distance of 30 cm.
Step 7: Calculate the height of the image (h_i) using magnification
The magnification (M) is given by:
M=hiho=−vu
Substituting the known values:
M=−−30−30=−1
Step 8: Find the height of the image
Using the magnification:
hi4=−1
Cross-multiplying gives:
hi=−4cm
Step 9: Interpret the height of the image
The negative sign indicates that the image is inverted. Thus, the length of the image is 4 cm.
Final Answers:
a. The image is formed at a distance of 30 cm in front of the mirror.
b. The length of the image is 4 cm (inverted).
---
- Length of the object (h_o) = 4 cm
- Object distance (u) = -30 cm (negative due to sign convention)
- Focal length (f) = -15 cm (negative for concave mirror)
The mirror formula is given by:
1v+1u=1f
1v+1−30=1−15
Rearranging gives:
1v=1−15+130
The common denominator for -15 and 30 is 30:
1−15=−230
So,
1v=−230+130=−2+130=−130
Taking the reciprocal gives:
v=−30cm
The negative sign indicates that the image is formed in front of the mirror, at a distance of 30 cm.
The magnification (M) is given by:
M=hiho=−vu
M=−−30−30=−1
Using the magnification:
hi4=−1
hi=−4cm
The negative sign indicates that the image is inverted. Thus, the length of the image is 4 cm.
a. The image is formed at a distance of 30 cm in front of the mirror.
b. The length of the image is 4 cm (inverted).
Topper's Solved these Questions
- BOOK - ICSECHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISE 7(B)9videos
REFLECTION OF LIGHT
- BOOK - ICSECHAPTER - PROPAGATION OF SOUND WAVES EXERCISE - EXERCISE -8(B) (Multiple choice type)3videos
PROPAGATION OF SOUND WAVES
- BOOK - ICSECHAPTER - SOUNDEXERCISE - TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)3videos
SOUND
Similar Questions
A point light source is kept in front of a convex mirror at a distance of 40 cm. The focal length of the mirror is 40 cm. Find the position of image.
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
Q. Image formed by mirror isView SolutionAn object is placed at a distance of 48 cm in front of a concave mirror of focal length 24 cm.
a. Find the position of image.
b. What will be the nature of image?View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
Find the position of the image period.View SolutionAn object of height 2 cm is placed at a distance 20cm in front of a concave mirror of focal length 12 cm. Find the position, size and nature of the image
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
What will be the nature of the image?View SolutionA square ABCD of side 1mm is kept at distance 15cm in front of the concave mirror as shown in Figure. The focal length of the mirror is 10cm. The length of the perimeter of its image will be
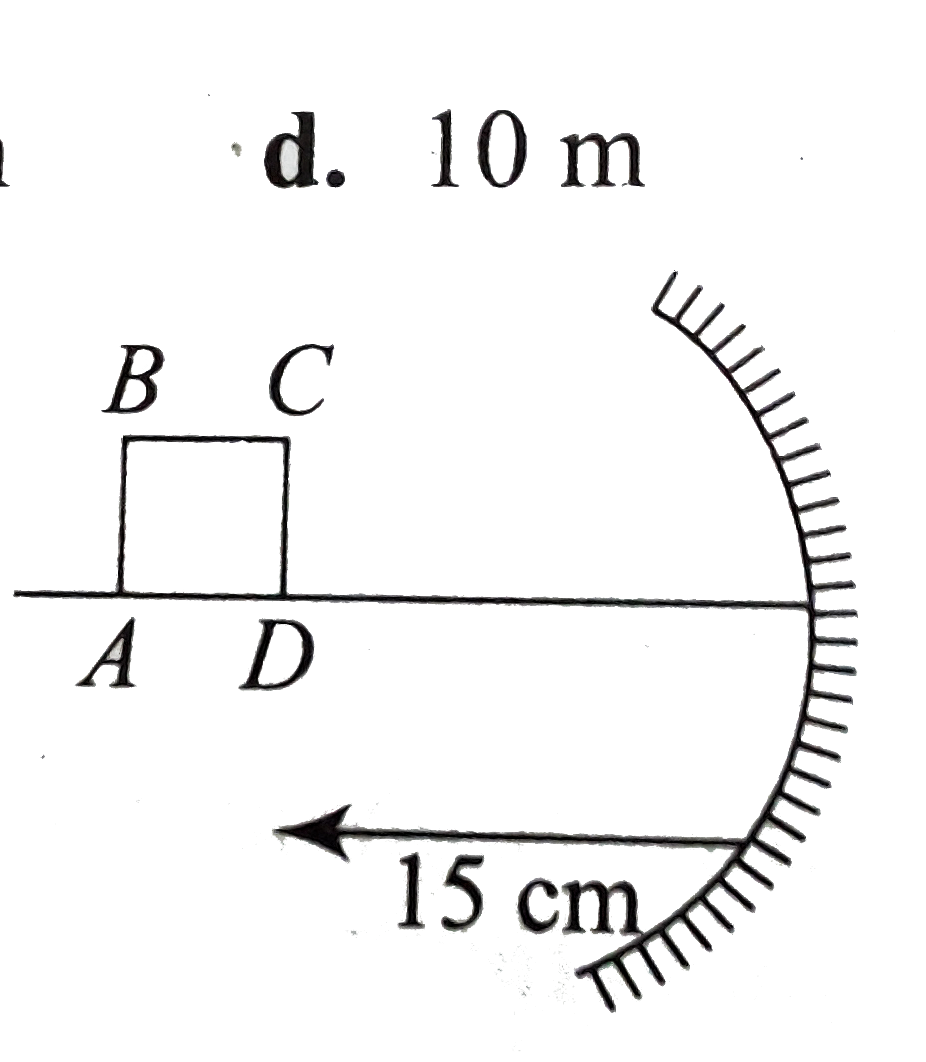 View Solution
View SolutionAn object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View Solution

