Find the position of the centre of a system of parallel forces applied to a rigid body.
The correct Answer is:x0=F1x1+F2x2+F3x3+……F1+F2+F3+….
Let the x-axis pass through the points of application of the forces, A1 and A2, with the coordinates x1 and x2, the coordinate of the centre O being x0. Then l1=x0−x1,l2=x2 x0. Substituting this into the result of the previous problem, we obtain: F1(x0−x1)=
=F2(x2−x0), whence
x0=F1x1+F2x2F1+F2
The position of the centre of several parallel forces may be found by using the method of complete induction.
Similar Questions
Find out the position of centre of mass of two particle system.
View SolutionTwo parallel forces F1 and F2 acting in the same direction are applied to a rigid body.
Porve that
(a) the magnitude of the resultant force is equal to the sum of magnitudes of the forces being added,
(b) the resultant force is parallel to the forces being added and acts in the same direction,
(c ) the resultant force passes through the centre of the parallel forces, i.e. through the point which divides the distance between the points of application of both forces into sections inversely proportional to the magnitude of the forces.
View Solution
Knowledge Check
When a constant torque is applied on a rigid body, then
Athe body moves with linear accelerationBthe body rotates with constant angular velocityCthe body rotates with constant angular accelerationDthe body undergoes equal angular displacement in equal intervals of timeThe centre of mass of rigid body cannot lie
Ainside the body alwaysBoutside the body always.Calways on its surfaceDat two points.S1: Net torque on a system due to all internal force about any point is zero.
S2: For rigid body undergoing fixed axis rotation, the direction of its angular acceleration and angular velocity
S3: if net torque on a rigid body about its centre of mass is zero, the angular speed of the rigid body is always zero.
S4: For a rigid body undergoing fixed axis rotation abouts its centre of mass, then net torque on rigid body about any point is same.ATFFFBTTFTCFFFFDTFFT
If some mass of area is removed from a rigid body, then the position of centre of mass of the remaining postion is obtained from the following formulae.
View SolutionS1: Net torque on a system due to all internal force about any point is zero.
S2: For rigid body undergoing fixed axis rotation, the direction of its angular acceleration and angular velocity
S3: if net torque on a rigid body about its centre of mass is zero, the angular speed of the rigid body is always zero.
S4: For a rigid body undergoing fixed axis rotation abouts its centre of mass, then net torque on rigid body about any point is same.
View SolutionOn what factors does the position of cm of a rigid body depend ?
View SolutionWhat is the effect of force on a rigid body ?
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
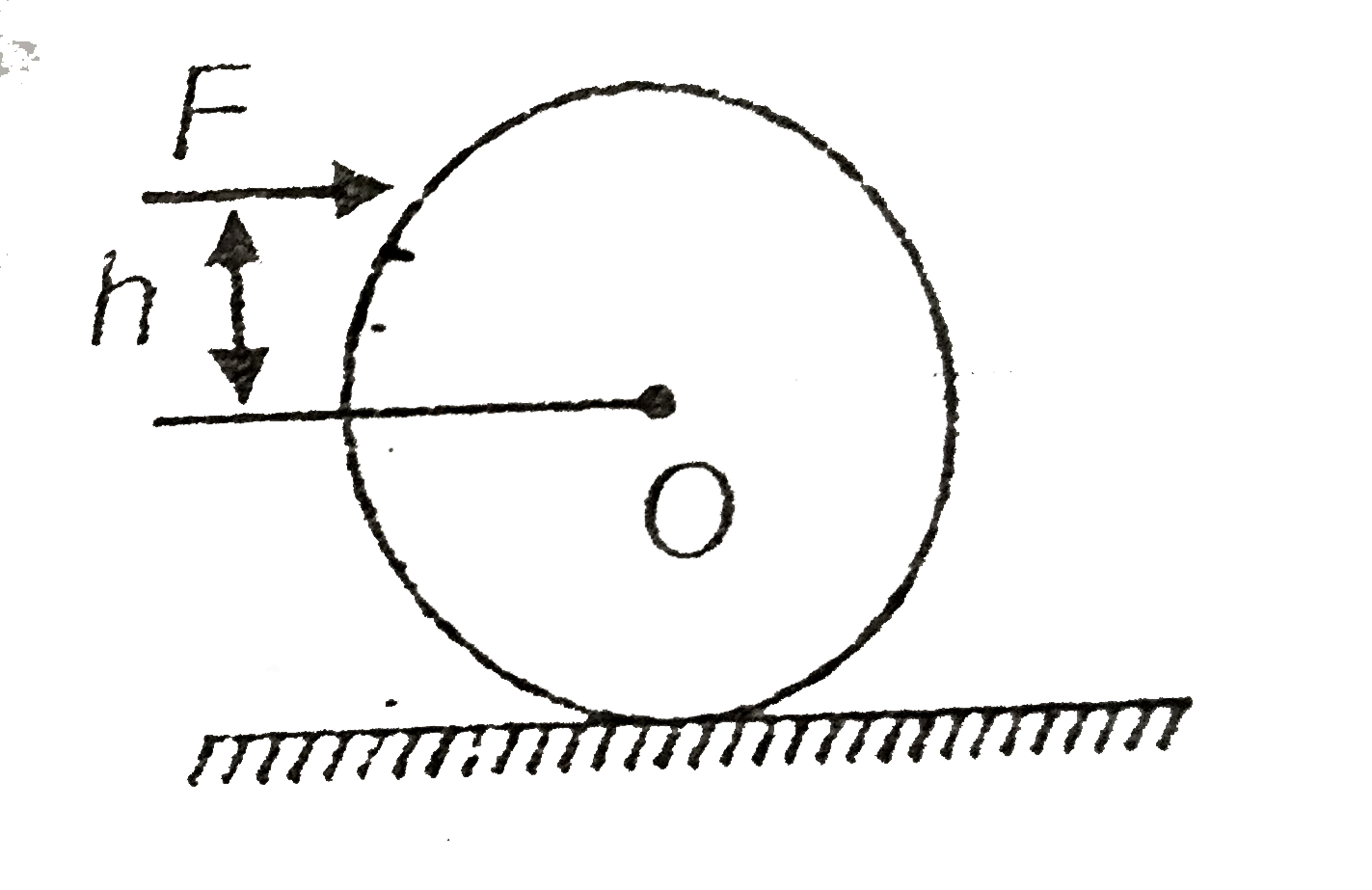
View Solution
