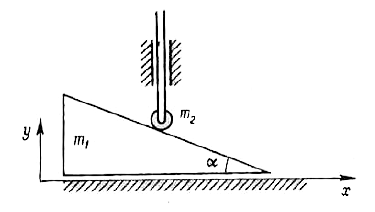
A rod of mass $m_{2}$ rests on wedge of mass $m_{1}$ (Fig.). Guides allow the rod to move only in the direction of the y-axis and the wedge only in the direction of the x-axis. Find the acceleration of both bodies and the reaction of the wedge. Neglect friction.

Text Solution

Verified by Experts

The correct Answer is: $a_{1} = - g = \frac{m_{3}}{m_{2} tan α + m_{1} cot α}, a_{2} = - g \frac{m_{2} tan α}{m_{2} tan α + m_{1} cot α}, Q = \frac{m_{1} m_{2} g cos α}{m_{2} {sin}^{2} α + m_{1} {cos}^{2} α}$ .

Three forces act on the rod: the reaction of the wedge Q, the reaction of the guides F and the gravitational force $m_{2} g$ (Fig.). The equation of motion (in the y-direction) is
$- m_{2} g + Q cos α = m_{2} a_{2}$
Correspondingly, three forces also act on the wedge: the reaction of the table N, the gravitational force $m_{1} g$ , and the reaction of the rod Q

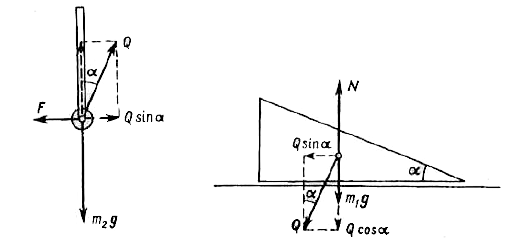
(Fig). The equation of motion (in the x-direction) is
$- Q sin α = m_{1} a_{1}$
To obtain the third equation, we compare the displacements of the rod $Δ y = 1 / 2 a_{2} t^{2}$ with that of the wedge $Δ x = 1 / 2 a_{1} t^{2}$ . Since $Δ y = Δ x tan α$ it follows that
$a_{2} = a_{1} tan α$
Then we solve the system of three equations with three unknowns.

|

Class 12 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

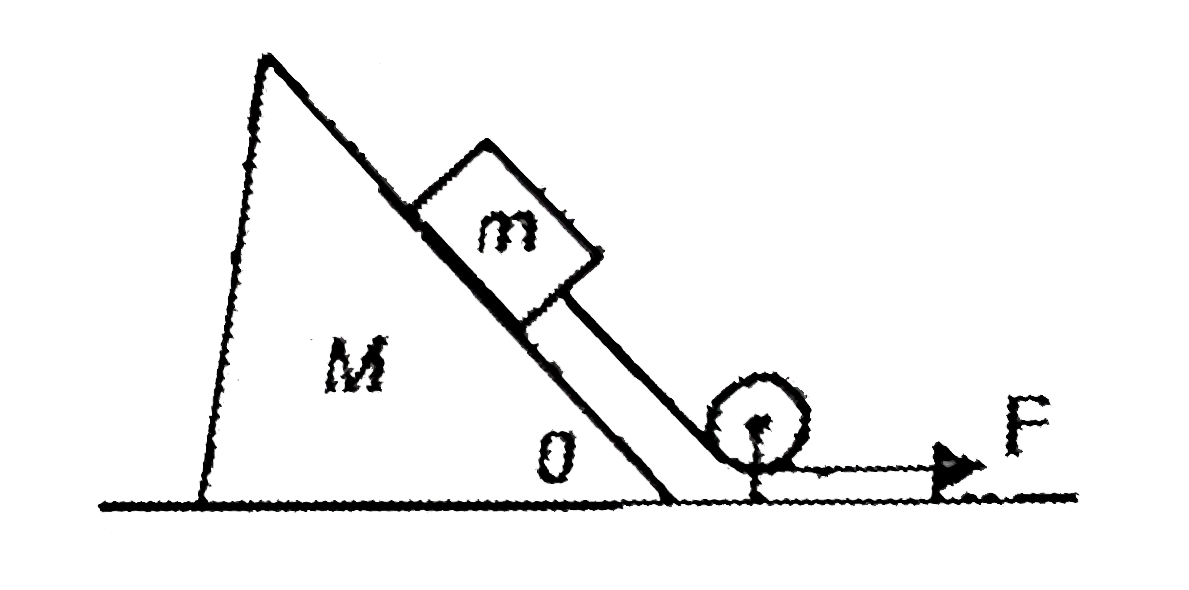
In fig. mass $m$ is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

A $a = \frac{F (1 - cos θ) m g 2 sin θ cos θ}{M + 2 m {sin}^{2} θ}$
B $a = \frac{F (1 + cos θ) + m g sin θ cos θ}{M + m {sin}^{2} θ}$
C $a = \frac{F (1 - cos θ) - m g sin θ cos θ}{M + m {sin}^{2} θ}$
D $a = \frac{F (1 + cos θ) - m g sin θ cos θ}{M - m {sin}^{2} θ}$
In the system shown, the initial acceleration of the wedge of mass 5M is (there is no friction anywhere)

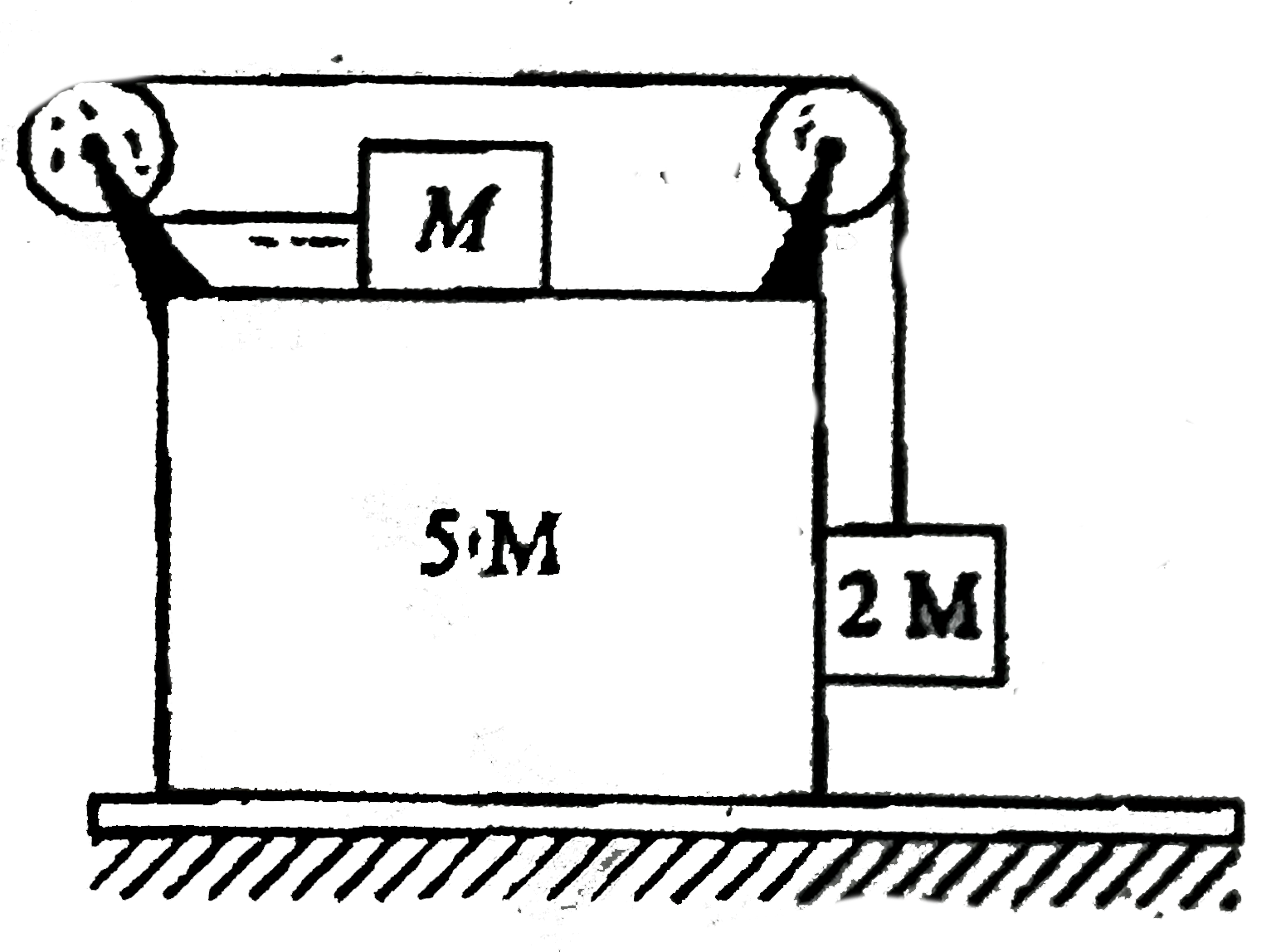Azero
B $g / 2$
C $g / 3$
D $g / 4$

Recommended Questions

Home
Ask Doubt
Profile