Find the period of revolution of a conical simple pendulum whose thread of length l makes an angle α with the vertical (Fig).

The correct Answer is:T=2π√lcosαg
Similar Questions
A conical pendulum of length L makes an angle θ with the vertical. The time period will be

View SolutionWhat is the torque acting on the bob of mass m of a simple pendulum Of length l, when the string of the pendulum makes an angle θ with the vertical ? When is the torque (i) zero and (ii) maximum.
View Solution
Knowledge Check
A conical pendulum of length L makes an angle θ with the vertical. The time period will be
 A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√LgtanθA simple pendulum is set up in a trolley which moves to the right with an acceleration a on a horizontal plane. Then the thread of the pendulum in the mean position makes an angle θ with the vertical
Atan−1(ag) in the forward directionBtan−1(ag) in the backward directionCtan−1(ga) in the backward directionDtan−1(ga) in the forward directionIf T and T' are the periods of a simple pendulum and a conical pendulum of the sample length then .
AT=T'BT<T'CT>T'DT=12T'
What is the period of a simple pendulum whose length is 50 cm?
View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)

View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
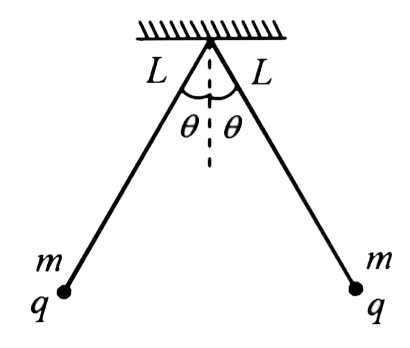
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.

View SolutionA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View Solution
