With the aid of numerical calculation find the instantaneous values of the acceleration and the speed of the falling ball in the previous problem and plot the graph. Choose an interval of time equal to Δt=0.02s.
From the law of motion we obtain the law of the variation of acceleration with speed:
a=5.10−22.5v
For small time intervals (Δt−0.02s)
vn=vn−1+an−1Δt
We can now compute Table 5.13 and draw the graph (Fig.). From them it may be seen that the stationary speed is v = 0.227 m/s, the transient period is τ=0.22s
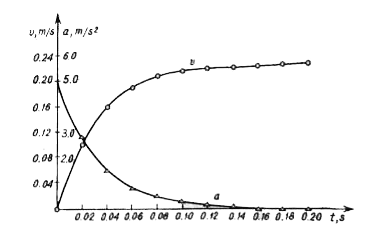
(where an approximate solution based on the assumption of uniformly accelerated motion was discused).

Similar Questions
Knowledge Check
Assertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are falseIn the previous problem if the car is moving with a constant acceleration of 2m/s2, the ball will fall behind the person at a distance
A32mB64mC96mD16m
Draw a graph for acceleration against time for a uniformly accelerated motion. How can it be used to find the change in speed in a certain interval of time?
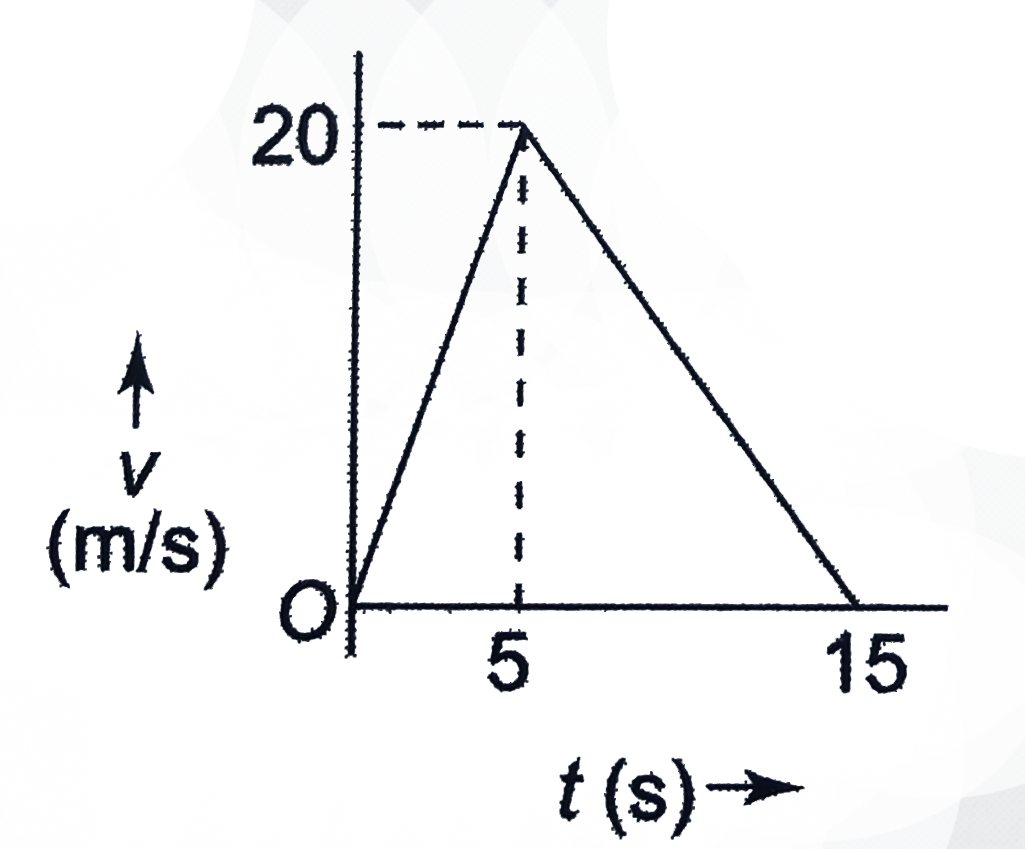
View SolutionFrom the following v-t graph, find the displacement for time interval t=3 to t=12s.
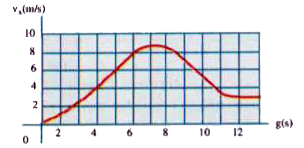
View SolutionGraph of velocity (v) versus time 't' for motion of a motorbike which starts from rest and moves along a stright road is given .
(a)Find the average acceleration for the time interval t0=0 to t1=6.0 s
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration is zero ?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
View SolutionAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.
View SolutionFind average speed in time interval t= 2 to t=10s
View SolutionSuppose the ceiling in the previous problem is that the elevator which is going up with an acceleration of 2.0ms2. Find the elongations.
View Solution
