Doubtnut Promotions Sticky

Prove that as a result of an elastic collision of two nonrelativistic particles of equal mass the scattering angle will be 90°.

Text Solution
Verified by Experts

ln the given reference frame one of the particles is at rest before the impact. the other moves at a speed v. After the collision their velocities are v 1 and v 2 , respectively. the scattering angle is a (Fig. 10.5a). Construct a triangle of momenta (Fig. 10.5b). Taking account or the fact. that tho total momentum and lho total kinetic energy are retained after an elastic collision, we obtain
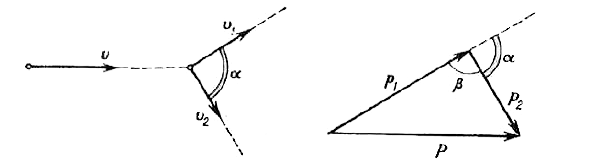
ocr_image
p 2 = p 1 2 + p 2 2 - 2 p 1 p 2 cos β , p 2 2 m = p 1 2 2 m + p 2 2 2 m
Hence cos β = 0 and α = β = 90 ∘

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12PHYSICSCENTRE OF MASS

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    In an elastic collision between two particles

    Anet external force is zero
    Bthe kinetic energy of the system before collision is equal to the kinetic of the system after collision.
    Clinear momentum of system before collision = linear momentum after collision
    Dthe total energy of the system is never conserved.
  • Question 2 - Select One or More

    In an elastic collision between two particles

    Athe total kinetic energy of the system is always conserved.
    Bthe kinetic energy of the system before collision is equal to the kinetic energy of the system after collision.
    Cthe linear momentum of the system is conserved.
    Dthe mechanical energy of the system before collision is equal to the mechanical energy of the system after collision.
  • Question 3 - Select One

    In head on elastic collision of two bodies of equal masses, it is not possible :

    Athe velocities are interchanged
    Bthe speeds are interchanged
    Cthe momenta are interchanged
    Dthe faster body speeds up and the slower body slows down