A ball is thrown horizontally at a speed v0 from the top of a hill whose slope is a (to the horizontal). Assuming the ball's impact on the hill's surface to be elastic find the point where it will hit the hill the second time.
The correct Answer is:The ratio of the distances is t2/t1=1+2sin2α.
Arrange the coordinate axes as shown in Fig. 10.11. Then com ponants of the initial velocity along the axes will be v0x=v0cosα,v0y=v0sinα and the acceleration components will be ax=gsinα,ay=−gcosα. The equation of motion for the first part of the tra- jectory should be written thus:
vx=v0xaxt=v0cosα+>sinα
vy=v0y+ayt=v0sinα−>cosα
x=x0+v0xt+axt22=v0tcosα+>2sinα2
y=y0+v0yt+ayt22=v0tsinα−>2cosα2
Since at the point A1 the cordinate y1=0, it follows that
t1=2v0tanαg,x1=2v20sinαgcos2α
v1x=v0cosα(1+sin2α),v1y−v0sinα
The longitudinal velocity component does not change- after an elastic impact, but the lateral component changes sign. Therefore

for the second part of the trajectory
v0x=v1x=v0cosα(1+sin2α)(1+sin2α),v0y=−v1y=v0sinα
The equation of motion, by analogy with the first case, will be
x=x1+v0xt+axt22=2v20sinαgcos2α+v0t(1+sin2α)cosα+>2sinα2
y=y1+v20y+ayt22=v0tsinα−>2cosα2
At the point A2 the ordinate is again zero, i.e. y2=0, therefore the x-coordinate of the point A2 is
x2=4v20sin2αgcos2α(1+sin2α)
The ratio of displacements is
l2l1=x2−x1x1=1+2sin2α
Similar Questions
A ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
View SolutionA ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both the balls reach the ground at the same time ?
View Solution
Knowledge Check
A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Time taken by the ball to strike the ground isA√20sB2√20sC4√20sD10sA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
A2v2gB√2[2v2g]Cv2gD√2v2g
A man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.
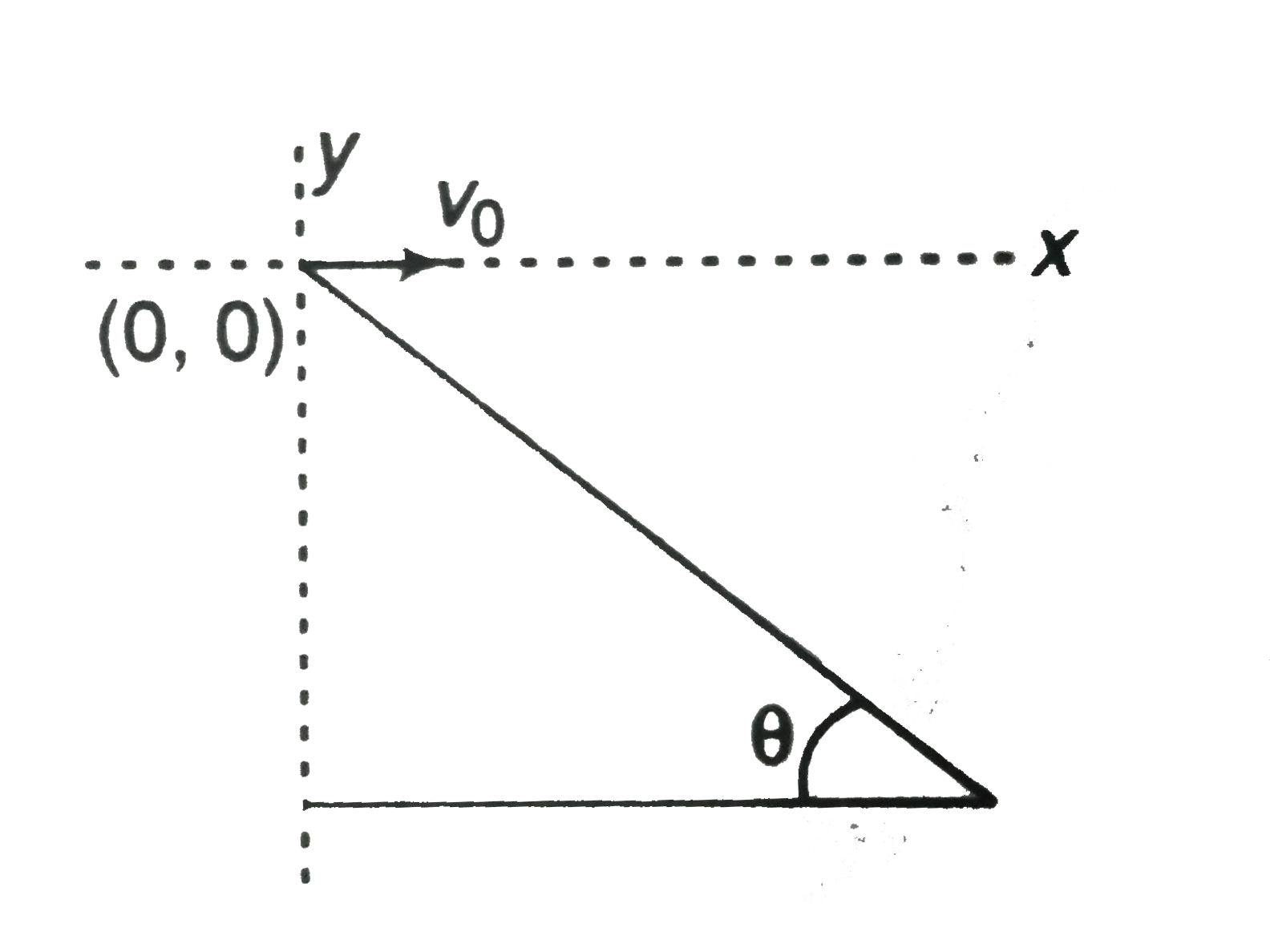
View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.

View SolutionA man standing on a hill top projects a stone horizontally with speed v0 as shown in figure. Taking the co-ordinate system as given in the figure. Find the co-ordinates of the point where the stone will hit the hill surface.

View SolutionA ball thrown horizontally with velocity v from the top of a tower of height h reaches the ground in t second.If another ball of double mass is thrown horizontally with velocity 2v from the top of another tower of height 9h then it reaches the ground in time (second)?
View SolutionA ball is thrown horizontally from the top of a lower of unkown height .Ball strikes a vertical wall whose plane is normal to the plane of month of ball Collison is elastic and ball falls on ground exactly at the midpoints between the lower and the wall ball strikes the grouind at an angle of the 30∘ with horizontal .Find the hieght of the tower (in meter)
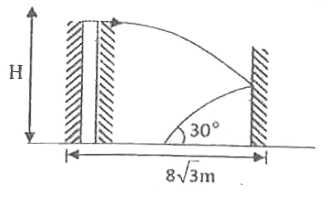
View SolutionA ball is thrown horizontally from the top of a lower of unkown height .Ball strikes a vertical wall whose plane is normal to the plane of month of ball Collison is elastic and ball falls on ground exactly at the midpoints between the lower and the wall ball strikes the grouind at an angle of the 30∘ with horizontal .Find the hieght of the tower (in meter)

View Solution
